
 ,
,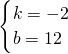 .
. p(-2p+12)=-p2+6p=-(p-3)2+9,
p(-2p+12)=-p2+6p=-(p-3)2+9, t,OG=t+2
t,OG=t+2 t,GE2=2t,
t,GE2=2t, t,OH=6-t-
t,OH=6-t- t,HF2=t,
t,HF2=t, t,2t),
t,2t), t,t).
t,t). x-
x- t,
t, ×(6-t)-
×(6-t)- t,
t,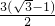 ;
; x+4t+
x+4t+ t,
t, ×(6-t)+4t+
×(6-t)+4t+ t,
t, ;
; -
- t,OG=6
t,OG=6 -
- t+t,GE2=6-t,
t+t,GE2=6-t, t,OH=6-t-
t,OH=6-t- t,HF2=t,
t,HF2=t, -
- t+t,6-t),
t+t,6-t), t,t).
t,t). x-
x- t,
t, ×(6-t)-
×(6-t)- t,
t,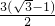 ,不符合2<t≤4;
,不符合2<t≤4;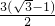 或
或 或3.
或3.

科目:初中數學 來源: 題型:
 已知1月、7月、9月和12月這四個月的月平均價格分別為8元/千克、26元/千克、14元/千克、11元/千克.
已知1月、7月、9月和12月這四個月的月平均價格分別為8元/千克、26元/千克、14元/千克、11元/千克.查看答案和解析>>
科目:初中數學 來源: 題型:
 探照燈、鍋蓋天線、汽車燈等都利用了拋物線的一個原理:由它的焦點處發出的光線被反射后將會被平行射出.如圖,由焦點O處發出的光線OB,OC經反射后沿與POQ平行的方向射出,已知∠ABO=42°,∠DCO=53°,則∠BOC=
探照燈、鍋蓋天線、汽車燈等都利用了拋物線的一個原理:由它的焦點處發出的光線被反射后將會被平行射出.如圖,由焦點O處發出的光線OB,OC經反射后沿與POQ平行的方向射出,已知∠ABO=42°,∠DCO=53°,則∠BOC=查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知1月、7月、9月和12月這四個月的月平均價格分別為8元/千克、26元/千克、14元/千克、11元/千克.
已知1月、7月、9月和12月這四個月的月平均價格分別為8元/千克、26元/千克、14元/千克、11元/千克.查看答案和解析>>
科目:初中數學 來源:2013年初中畢業升學考試(甘肅蘭州卷)數學(解析版) 題型:解答題
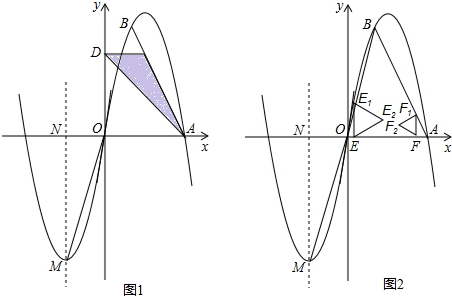
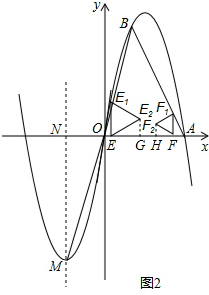
如圖,在平面直角坐標系 中,A、B為x軸上兩點,C、D為y軸上的兩點,經
中,A、B為x軸上兩點,C、D為y軸上的兩點,經
過點A、C、B的拋物線的一部分C1與經過點A、D、B的拋物線的一部分C2組合成一條封閉曲線,我們把這條封
閉曲線稱為“蛋線”.已知點C的坐標為(0, ),點M是拋物線C2:
),點M是拋物線C2: (
( <0)的頂點.
<0)的頂點.

(1)求A、B兩點的坐標;
(2)“蛋線”在第四象限上是否存在一點P,使得△PBC的面積最大?若存在,求出△PBC面積的最大值;若不存在,請說明理由;
(3)當△BDM為直角三角形時,求 的值.
的值.
查看答案和解析>>
科目:初中數學 來源:2012年湖北省鄂州市梁子湖區中考數學模擬試卷(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com