
【題目】如圖,在矩形![]() 中,
中,![]() ,
,![]() ,反比例函數
,反比例函數![]() (
(![]() )的圖像與矩形兩邊AB、BC分別交于點D、點E,且
)的圖像與矩形兩邊AB、BC分別交于點D、點E,且![]() .
.
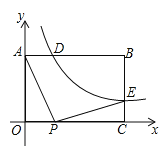
(1)求點D的坐標和![]() 的值;
的值;
(2)求證:![]() ;
;
(3)若點![]() 是線段
是線段![]() 上的一個動點,是否存在點
上的一個動點,是否存在點![]() ,使
,使![]() ?若存在,求出此時點
?若存在,求出此時點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)![]() ,4;(2)見解析;(3)存在點
,4;(2)見解析;(3)存在點![]() ,
,![]() 或
或![]() .
.
【解析】
(1)由矩形OABC中,AB=4,BD=2AD,可得3AD=4,即可求得AD的長,然后求得點D的坐標,即可求得k的值,繼而求得點E的坐標;
(2)由E點在反比例函數![]() 圖像上,可求E點坐標,進而求出EC的長即可求證.
圖像上,可求E點坐標,進而求出EC的長即可求證.
(3)首先假設存在要求的點P坐標為(m,0),OP=m,CP=4-m,由∠APE=90°,易證得△AOP∽△PCE,然后由相似三角形的對應邊成比例,求得m的值,繼而求得此時點P的坐標.
解:(1)在矩形![]() 中,
中,![]() 軸,且
軸,且![]() ,
,

∴點![]() 的縱坐標為3.
的縱坐標為3.
∵![]() ,且
,且![]() ,
,
![]() ,
,
∴![]() .
.
∴點![]() 在反比例函數
在反比例函數![]() 圖像上,
圖像上,
∴![]() .
.
(2)證:∵![]() 在
在![]() 上,
上,
∴![]() 橫坐標為4,
橫坐標為4,
在![]() 中,當
中,當![]() 時,
時,![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)存在點![]() ,使
,使![]() ,其過程是:
,其過程是:
設![]() ,則
,則![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,即
,即![]() .解得
.解得![]() 或
或![]() .
.
![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,給出如下定義:已知兩個函數,如果對于任意的自變量![]() ,這兩個函數對應的函數值記為
,這兩個函數對應的函數值記為![]() , 恒有點
, 恒有點![]() 和點
和點![]() 關于點
關于點![]() 成中心對稱(此三個點可以重合),由于對稱中心
成中心對稱(此三個點可以重合),由于對稱中心![]() 都在直線
都在直線![]() 上,所以稱這兩個函數為關于直線
上,所以稱這兩個函數為關于直線![]() 的“相依函數”。例如:
的“相依函數”。例如: ![]() 和
和![]() 為關于直線
為關于直線![]() 的 “相依函數”.
的 “相依函數”.
(1)已知點![]() 是直線
是直線![]() 上一點,請求出點
上一點,請求出點![]() 關于點
關于點![]() 成中心對稱的點
成中心對稱的點![]() 的坐標:
的坐標:
(2)若直線![]() 和它關于直線
和它關于直線![]() 的“相依函數”的圖象與
的“相依函數”的圖象與![]() 軸圍成的三角形的面積為
軸圍成的三角形的面積為![]() ,求
,求![]() 的值;
的值;
(3)若二次函數![]() 和
和![]() 為關于直線
為關于直線![]() 的“相依函數”.
的“相依函數”.
①請求出![]() 的值;
的值;
②已知點![]() 、點
、點![]() 連接
連接![]() 直接寫出
直接寫出![]() 和
和![]() 兩條拋物線與線段
兩條拋物線與線段![]() 有目只有兩個交占時對應的
有目只有兩個交占時對應的![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=ax2+bx+c交x軸于A(﹣1,0),B(3,0),交y軸的負半軸于C,頂點為D.下列結論:①2a+b=0;②2c<3b;③當m≠1時,a+b<am2+bm;④當△ABD是等腰直角三角形時,則a=![]() ;⑤當△ABC是等腰三角形時,a的值有3個.其中正確的有( )個.
;⑤當△ABC是等腰三角形時,a的值有3個.其中正確的有( )個.

A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“食品安全”受到全社會的廣泛關注,育才中學對部分學生就食品安全知識的了解程度,采用隨機抽樣調查的方式,并根據收集到的信息進行統計,繪制了下面的兩幅尚不完整的統計圖,請你根據統計圖中所提供的信息解答下列問題:
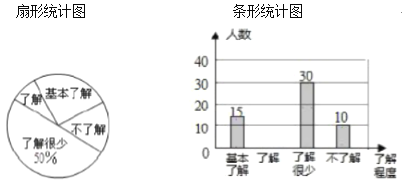
(1)接受問卷調查的學生共有________人,扇形統計圖中“基本了解”部分所對應扇形的圓心角為_________![]() ;
;
(2)請補全條形統計圖;
(3)若對食品安全知識達到“了解”程度的學生中,男、女生的比例恰為![]() ,現從中隨機抽取
,現從中隨機抽取![]() 人參加食品安全知識競賽,則恰好抽到
人參加食品安全知識競賽,則恰好抽到![]() 個男生和
個男生和![]() 個女生的概率________.
個女生的概率________.
查看答案和解析>>
科目:初中數學 來源: 題型:
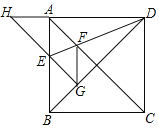
【題目】如圖,正方形ABCD的邊長為1,AC、BD是對角線,將△DCB繞著點D順時針旋轉45°得到△DGH,HG交AB于點E,連接DE交AC于點F,連接FG.則下列結論:①四邊形AEGF是菱形;②△HED的面積是1﹣![]() ;③∠AFG=135°;④BC+FG=
;③∠AFG=135°;④BC+FG=![]() .其中正確的結論是_____.(填入正確的序號)
.其中正確的結論是_____.(填入正確的序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A點的坐標為(﹣1,5),B點的坐標為(3,3),C點的坐標為(5,3),D點的坐 標為(3,﹣1),小明發現:線段AB與線段CD存在一種特殊關系,即其中一條線段繞著某點旋轉一個角度可以得到另一條線段,你認為這個旋轉中心的坐標是_____________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四邊形ADEF是正方形,點B、C分別在邊AD、AF上,此時BD=CF,BD⊥CF成立.

(1)當△ABC繞點A逆時針旋轉θ(0°<θ<90°)時,如圖2,BD=CF成立嗎?若成立,請證明;若不成立,請說明理由.
(2)當△ABC繞點A逆時針旋轉45°時,如圖3,延長DB交CF于點H.
①求證:BD⊥CF;
②當AB=2,AD=3![]() 時,求線段DH的長.
時,求線段DH的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一個有45°角的三角板的直角頂點放在一張寬為3cm的紙帶邊沿上,另一個頂
點在紙帶的另一邊沿上,測得三角板的一邊與紙帶的一邊所在的直線成30°角,如圖(3),
則三角板的最大邊的長為( )
A. ![]() B.
B. ![]() C.
C.![]()
![]() D.
D. ![]()
![]()

查看答案和解析>>
科目:初中數學 來源: 題型:
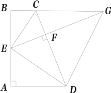
【題目】如圖,已知四邊形ABCD中,AB⊥AD,BC∥AD,E為AB的中點,且EC、ED分別為∠BCD、∠ADC的角平分線,EF⊥CD交BC的延長線于點G,連接DG.
(1)求證:CE⊥DE;
(2)若AB=6,求CF·DF的值;
(3)當△BCE與△DFG相似時,![]() 的值是 .
的值是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com