
【題目】如圖,點P是∠MON內的一點,過點P作PA⊥OM于點A,PB⊥ON于點B,且OA=OB.
(1)求證:PA=PB;
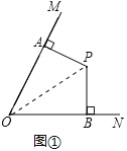
(2)如圖②,點C是射線AM上一點,點D是線段OB上一點,且∠CPD+∠MON=180°,若OC=8,OD=5.求線段OA的長.
(3)如圖③,若∠MON=60°,將PB繞點P以每秒2°的速度順時針旋轉,12秒后,PA開始繞點P以每秒10°的速度順時針旋轉,PA旋轉270°后停止,此時PB也隨之停止旋轉.旋轉過程中,PA所在直線與OM所在直線的交點記為G,PB所在直線與ON所在直線的交點記為H.問PB旋轉幾秒時,PG=PH?
【答案】(1)見解析;(2)OA=6.5;(3)滿足條件的t的值為15s或25s或37.5s.
【解析】
(1)如圖1中,連接OP,證明Rt△OPA≌Rt△OPB(HL)即可解決問題.
(2)如圖②中,想辦法證明OC+OD=2OA即可解決問題.
(3)設點P的旋轉時間為t秒.分四種情形①當0<t<12時,不存在.②當12≤t<21時,如圖3-1中.③當21≤t<30時,如圖3-2中.④當30≤t<39時,如圖3-3中,分別求解即可解決問題.
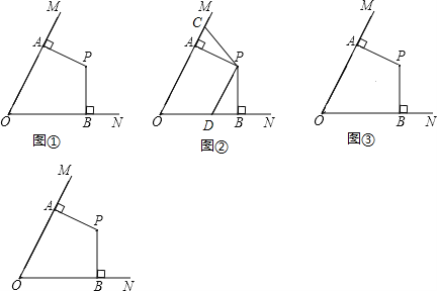
(1)證明:如圖①中,連接OP.
∵PA⊥OM,PB⊥ON,
∴∠OAP=∠OBP=90°,
∵OA=OB,OP=OP,
∴Rt△OPA≌Rt△OPB(HL),
∴PA=PB.
(2)如圖②中,
∵∠PAO=∠PBO=90°,
∴∠AOB+∠APB=180°,
∵∠CPD+∠AOB=180°,
∴∠CPD=∠APB,
∴∠APC=∠BPD,
∵PA=PB,∠PAC=∠PBD=90°,
∴△PAC≌△PBD(ASA),
∴AC=BD,
∴OC+OD=OA+AC+OB-BD=2OA=13,
∴OA=6.5.
(3)設點P的旋轉時間為t秒.
①當0<t<12時,此時只有PB旋轉,PA沒有旋轉,故不存在PG=PH.
②當PA旋轉的度數為0°—90°時,時間t的取值為:12≤t<21;
∴當12≤t<21時,如圖3-1中,∠APG=(10t-120)°,∠BPH=2t°,
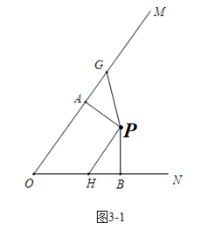
當∠APG=∠BPH時,△PAG≌△PBH,可得PG=PH,
此時10t-120=2t,
∴t=15.
③當PA旋轉的度數為90°—180°時,時間t的取值為:21≤t<30,
∴當21≤t<30時,如圖3-2中,∠APG=180°-∠APA′=180°-(10t-120)°=(300-10t)°,∠BPH=2t,
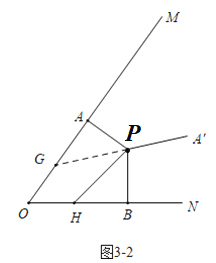
當∠APG=∠BPH時,△PAG≌△PBH,可得PG=PH,
此時300-10t=2t,
∴t=25.
④當PA旋轉的度數為180°—270°時,時間t的取值為:30≤t<39;
當30≤t<39時,如圖3-3中,∠APG=(10t-300)°,∠BPH=2t,
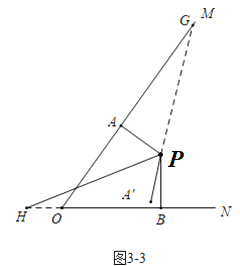
當∠APG=∠BPH時,△PAG≌△PBH,可得PG=PH,
此時10t-300=2t,
∴t=37.5;
綜上所述,滿足條件的t的值為15s或25s或37.5s.


科目:初中數學 來源: 題型:
【題目】如圖,菱形OABC的一邊OA在x軸的負半軸上,O是坐標原點,tan∠AOC=![]() ,反比例函數y=
,反比例函數y=![]() 的圖象經過點C,與AB交于點D,若△COD的面積為20,則k的值等于_____.
的圖象經過點C,與AB交于點D,若△COD的面積為20,則k的值等于_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數軸上,數![]() 所對應的點與原點的距離叫做數
所對應的點與原點的距離叫做數![]() 的絕對值,記作
的絕對值,記作![]()
提出問題:(1)點![]() 所表示的數如圖所示,則
所表示的數如圖所示,則![]() 兩點間的距離是 ,
兩點間的距離是 ,![]() 兩點間的距離是_____,
兩點間的距離是_____,![]() 兩點間的距離是 .
兩點間的距離是 .
探究結論:(2)在數軸上,若![]() 兩點對應的數分別是
兩點對應的數分別是![]() ,則
,則![]() ____ (用含有
____ (用含有![]() 的式子表示).
的式子表示).
拓展應用:(3)請利用.上述結論,解決下列問題:
①![]() 和
和![]() 在數軸上對應的點之間的距離為
在數軸上對應的點之間的距離為
②![]()
③滿足![]() 的未知數的值為
的未知數的值為

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某機動車出發前油箱內有油42L,行駛若干小時后,途中在加油站加油若干升,油箱中余油量Q(L)與行駛時間t(h)之間的函數關系如圖所示,根據圖回答問題:
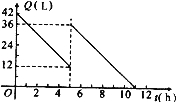
(1)機動車行駛 h后加油;
(2)加油前油箱余油量Q與行駛時間t的函數關系式是 ;
(3)中途加油 L;
(4)如果加油站距目的地還有230km,車速為40km/h,要到達目的地,油箱中的油是否夠用?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
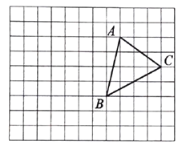
【題目】在如圖所示的方格紙中,小正方形的頂點叫做格點,![]() 是一個格點三角形(即
是一個格點三角形(即![]() 的三個頂點都在格點上),根據要求回答下列問題:
的三個頂點都在格點上),根據要求回答下列問題:
![]() 畫出
畫出![]() 先向左平移6格,再向上平移
先向左平移6格,再向上平移![]() 格所得的
格所得的![]() ;
;
![]() 利用網格畫出
利用網格畫出![]() 中
中![]() 邊上的高
邊上的高![]() .
.
![]() 過點
過點![]() 畫直線,將
畫直線,將![]() 分成面積相等的兩個三角形;
分成面積相等的兩個三角形;
![]() 畫出與
畫出與![]() 有一條公共邊,且與
有一條公共邊,且與![]() 全等的格點三角形.
全等的格點三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
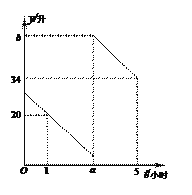
【題目】張師傅駕駛某種型號轎車從甲地去乙地,該種型號轎車每百公里油耗為10升(每行駛100公里需消耗10升汽油).途中在加油站加了一次油,加油前,根據儀表盤顯示,油箱中還剩4升汽油.假設加油前轎車以80公里/小時的速度勻速行駛,加油后轎車以90公里/小時的速度勻速行駛(不計加油時間),已知油箱中剩余油量y(升)與行駛時間t(小時)之間的函數關系如圖所示.
(1) 加油前,該轎車每小時消耗汔油 升;加油后,該轎車每小時消耗汔油 升;
(2)求加油前油箱剩余油量y(升)與行駛時間t(小時)之間的函數表達式;
(3)求張師傅在加油站加了多少升汽油.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形![]() 放置在平面直角坐標系上,點
放置在平面直角坐標系上,點![]() 分別在
分別在![]() 軸,
軸,![]() 軸的正半軸上,點
軸的正半軸上,點![]() 的坐標是
的坐標是![]() ,其中
,其中![]() ,反比例函數y=
,反比例函數y=![]()
![]() 的圖象交
的圖象交![]() 交于點
交于點![]() .
.
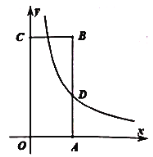
(1)![]() _____(用
_____(用![]() 的代數式表示)
的代數式表示)
(2)設點![]() 為該反比例函數圖象上的動點,且它的橫坐標恰好等于
為該反比例函數圖象上的動點,且它的橫坐標恰好等于![]() ,連結
,連結![]() .
.
①若![]() 的面積比矩形
的面積比矩形![]() 面積多8,求
面積多8,求![]() 的值。
的值。
②現將點![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到點
得到點![]() ,若點
,若點![]() 恰好落在
恰好落在![]() 軸上,直接寫出
軸上,直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 、
、![]() 的坐標分別為
的坐標分別為![]() ,
,![]() ,直線
,直線![]() 與
與![]() 軸交于點
軸交于點![]() 、與
、與![]() 軸交于點
軸交于點![]() .
.
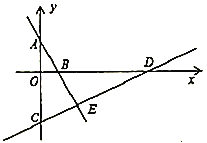
(1)直線![]() 解析式為
解析式為![]() ,求直線
,求直線![]() 與
與![]() 交點
交點![]() 的坐標;
的坐標;
(2)四邊形![]() 的面積是________;
的面積是________;
(3)求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】王紅有5張寫著以下數字的卡片,請按要求抽出卡片,完成下列各題:![]()
(1)從中取出2張卡片,使這2張卡片上數字乘積最小,最小值是 .
(2)從中取出2張卡片,使這2張卡片數字相除商最大,最大值是 .
(3)從中取出除0以外的4張卡片,將這4個數字進行加、減、乘、除或乘方等混合運算,使結果為24,(注:每個數字只能用一次,如:23×[1﹣(﹣2)]),請另寫出一種符合要求的運算式子 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com