
【題目】某機動車出發前油箱內有油42L,行駛若干小時后,途中在加油站加油若干升,油箱中余油量Q(L)與行駛時間t(h)之間的函數關系如圖所示,根據圖回答問題:
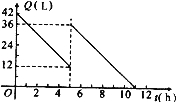
(1)機動車行駛 h后加油;
(2)加油前油箱余油量Q與行駛時間t的函數關系式是 ;
(3)中途加油 L;
(4)如果加油站距目的地還有230km,車速為40km/h,要到達目的地,油箱中的油是否夠用?請說明理由.
【答案】(1)5;(2)Q=42﹣6t(0≤t≤5);(3)24;(4)油箱中的油夠用.
【解析】
試題分析:(1)圖象上x=5時,對應著兩個點,油量一多一少,可知此時加油了;
(2)因為x=0時,Q=42,x=5時,Q=12,所以出發前油箱內余油量42L,行駛5h后余油量為12L,共用去30L,因此每小時耗油量為6L,由此即可寫出函數解析式;
(3)因為x=5時,y有兩個值12,36,所以加油(36﹣12)L;
(4)因為由圖象知,加油后還可行駛6小時,即可行駛40×6千米,然后同230千米做比較,即可求出答案.
試題解析:(1)5;
(2)∵出發前油箱內余油量42L,行駛5h后余油量為12L,共用去30L,
因此每小時耗油量為6L,
∴Q=42﹣6t(0≤t≤5);
(3)36﹣12=24,因此中途加油24L;
(4)由圖可知,加油后可行駛6h,
所以加油后行駛40×6=240km,
∵240>230,
∴油箱中的油夠用.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】某工藝廠計劃一周生產工藝品![]() 個,平均每天生產
個,平均每天生產![]() 個,但實際每天生產量與計劃相比有出入.下表是某周的生產情況(超產計為正、減產計為負):
個,但實際每天生產量與計劃相比有出入.下表是某周的生產情況(超產計為正、減產計為負):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
增減(單位:個) |
|
|
|
|
|
|
|
![]() 本周產量中最多的一天比最少的一天多生產多少個工藝品?
本周產量中最多的一天比最少的一天多生產多少個工藝品?
![]() 請求出該工藝廠在本周實際生產工藝品的數量;
請求出該工藝廠在本周實際生產工藝品的數量;
![]() 已知該廠實行每周計件工資制,每生產一個工藝品可得
已知該廠實行每周計件工資制,每生產一個工藝品可得![]() 元,若超額完成任務,則超過部分每個另獎
元,若超額完成任務,則超過部分每個另獎![]() 元.少生產一個扣
元.少生產一個扣![]() 元.試求該工藝廠在這一周應付出的工資總額.
元.試求該工藝廠在這一周應付出的工資總額.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,A(1,![]() ),B(2,0),C點在x軸上運動,過點O作直線AC的垂線,垂足為D.當點C在x軸上運動時,點D也隨之運動.則線段BD長的最大值為______________.
),B(2,0),C點在x軸上運動,過點O作直線AC的垂線,垂足為D.當點C在x軸上運動時,點D也隨之運動.則線段BD長的最大值為______________.
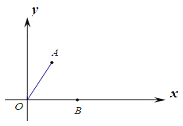
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,小明在A處利用測角儀觀測氣球C的仰角為30°,然后他沿正對氣球方向前進了40m到達B處,此時觀測氣球的仰角為45°.如果測角儀高度為1m,那么氣球的高度是多少?(精確到0.1m)(備注:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
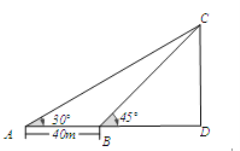
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國男性的體質系數計算公式是:m=![]() ×100%,其中W表示體重(單位:kg),H表示身高(單位:cm).通過計算出的體質系數m對體質進行評價.具體評價如下表:
×100%,其中W表示體重(單位:kg),H表示身高(單位:cm).通過計算出的體質系數m對體質進行評價.具體評價如下表:
m | <80% | 80%~90% | 90%~110% | 110%~120% | >120% |
評價結果 | 明顯消瘦 | 消瘦 | 正常 | 過重 | 肥胖 |
(1)某男生的身高是170cm,體重是75kg,他的體質評價結果是 ;
(2)現從某校九年級學生中隨機抽取n名男生進行體質評價,評價結果統計如下:
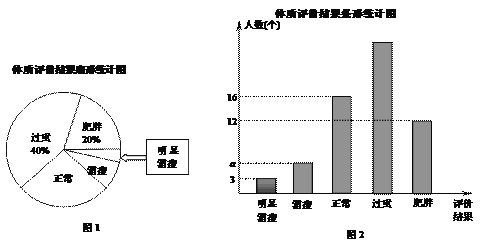
①抽查的學生數n= ;圖2中a的值為 ;
②圖1中,體質評價結果為“正常”的所在扇形圓心角為 °;
(3)若該校九年級共有男生480人,試估計該校九年級體質評價結果為“過重”或“肥胖”的男生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P是∠MON內的一點,過點P作PA⊥OM于點A,PB⊥ON于點B,且OA=OB.
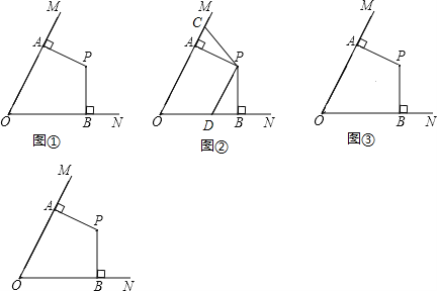
(1)求證:PA=PB;
(2)如圖②,點C是射線AM上一點,點D是線段OB上一點,且∠CPD+∠MON=180°,若OC=8,OD=5.求線段OA的長.
(3)如圖③,若∠MON=60°,將PB繞點P以每秒2°的速度順時針旋轉,12秒后,PA開始繞點P以每秒10°的速度順時針旋轉,PA旋轉270°后停止,此時PB也隨之停止旋轉.旋轉過程中,PA所在直線與OM所在直線的交點記為G,PB所在直線與ON所在直線的交點記為H.問PB旋轉幾秒時,PG=PH?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,邊長為1的正方形OA1B1C的對角線A1C和OB1交于點M1;以M1A1為對角線作第二個正方形A2A1B2M,對角線A1M1和A2B2交于點M2;以M2A1為對角線作第三個正方形A3A1B3M2,對角線A1M2和A3B3交于點M3;..依此類推,這樣作的第6個正方形對角線交點的坐標為____.
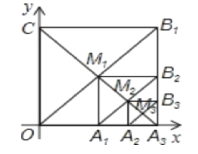
查看答案和解析>>
科目:初中數學 來源: 題型:
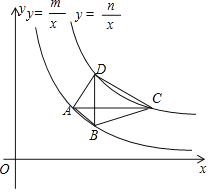
【題目】如圖,四邊形ABCD的四個頂點分別在反比例函數y=![]() 與y=
與y=![]() (x>0,0<m<n)的圖象上,對角線BD∥y軸,且BD⊥AC于點P.已知點B的橫坐標為4.
(x>0,0<m<n)的圖象上,對角線BD∥y軸,且BD⊥AC于點P.已知點B的橫坐標為4.
(1)當m=4,n=20時.
①若點P的縱坐標為2,求直線AB的函數表達式.
②若點P是BD的中點,試判斷四邊形ABCD的形狀,并說明理由.
(2)四邊形ABCD能否成為正方形?若能,求此時m,n之間的數量關系;若不能,試說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com