
【題目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 中點,
中點,![]() 為
為![]() 上一點(不與點
上一點(不與點![]() 、
、![]() 重合),連接
重合),連接![]() 、
、![]() 交于點
交于點![]() ,
,![]() .設
.設![]() ,
,![]() .則
.則![]() 關于
關于![]() 的函數解析式為_______.
的函數解析式為_______.
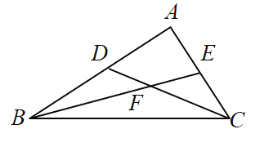
【答案】![]()
【解析】
過D點作DG⊥AB交BE與G,再通過說明△DGF為等腰三角形得到DG=GF;然后再說明DG=GF=![]() (4-x),G為BE的中點;再通過證明△EFC為等腰三角形得到EF=EC,進一步說明
(4-x),G為BE的中點;再通過證明△EFC為等腰三角形得到EF=EC,進一步說明
AE=2EG=4+x,最后運用勾股定理解答即可.
過D點作DG⊥AB交BE與G,
∴∠FDG+∠ADC=90°
又∵∠DFB+∠ADC=90°
∴∠FDG=∠DFB
∴△DGF為等腰三角形,
∴DG=GF
又∵在Rt△ABE中D為AB的中點,
∴DG為△ABE的中位線
∴DG=GF=![]() AE=
AE=![]() (4-x),G為BE的中點
(4-x),G為BE的中點
又∵在RT△ADC中∠ADC+∠ACD=90°
∴∠ACD=∠DFB
又∵∠DFB=∠EFC
∴∠ACD=∠EFC
∴△EFC為等腰三角形
∴EF=EC
∴EG=EF+GF=DG+EC=2+![]() x
x
∴BE=2EG=4+x
又∵△ABE為直角三角形
∴由勾股定理可的AB=![]()
∴![]()


科目:初中數學 來源: 題型:
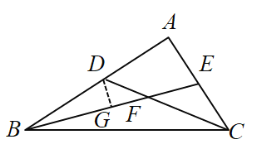
【題目】如圖①,在矩形ABCD中,AB<AD,對角線AC,BD相交于點O,動點P由點A出發,沿AB-BC→CD向點D運動設點P的運動路程為x,△AOP的面積為y,y與x的函數關系圖象如圖②所小示,則AD的長為________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() ,過
,過![]() 上到點
上到點![]() 的距離為1,3,5,7,…的點作
的距離為1,3,5,7,…的點作![]() 的垂線,分別與
的垂線,分別與![]() 相交,得到圖所示的陰影梯形,它們的面積依次記為
相交,得到圖所示的陰影梯形,它們的面積依次記為![]() ,
,![]() ,
,![]() ….則(1)
….則(1)![]() _______________;(2)通過計算可得
_______________;(2)通過計算可得![]() ______________.
______________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() 為邊
為邊![]() 上的中線,點
上的中線,點![]() 為
為![]() 延長線上一點,連接
延長線上一點,連接![]() 交
交![]() 于點
于點![]() ,
,![]() ,
,![]() .
.
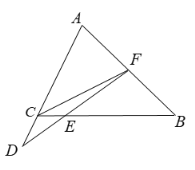
(1)求證:![]() ;
;
(2)在圖中找出與![]() 相等的線段,并證明;
相等的線段,并證明;
(3)若![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代數式表示).
的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
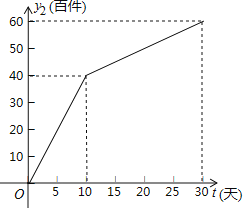
【題目】今年疫情防控期間,我市一家服裝有限公司生產了一款服裝,為對比分析以前實體商店和現在網上商店兩種途徑的銷售情況,進行了為期30天的跟蹤調查.其中實體商店的日銷售量![]() (百件)與時間
(百件)與時間![]() (
(![]() 為整數,單位:天)的部分對應值如下表所示;網上商店的日銷售量
為整數,單位:天)的部分對應值如下表所示;網上商店的日銷售量![]() (百件)與時間
(百件)與時間![]() (
(![]() 為整數,單位:天)的關系如圖所示.
為整數,單位:天)的關系如圖所示.
時間 | 0 | 6 | 10 | 12 | 18 | 20 | 24 | 30 |
日銷售量 | 0 | 72 | 100 | 108 | 108 | 100 | 72 | 0 |
(1)請你在一次函數、二次函數和反比例函數中,選擇合適的函數反映![]() 與
與![]() 的變化規律,并求出
的變化規律,并求出![]() 與
與![]() 的函數關系式及自變量
的函數關系式及自變量![]() 的取值范圍;
的取值范圍;
(2)求![]() 與
與![]() 的函數關系式,并寫出自變量
的函數關系式,并寫出自變量![]() 的取值范圍;
的取值范圍;
(3)在跟蹤調查的30天中,設實體商店和網上商店的日銷售總量為![]() (百件),求
(百件),求![]() 與
與![]() 的函數關系式;當
的函數關系式;當![]() 為何值時,日銷售量
為何值時,日銷售量![]() 達到最大,并求出此時的最大值.
達到最大,并求出此時的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b(k<0)與反比例函數![]() 的圖象相交于A、B兩點,一次函數的圖象與y軸相交于點C,已知點A(4,1)
的圖象相交于A、B兩點,一次函數的圖象與y軸相交于點C,已知點A(4,1)

(1)求反比例函數的解析式;
(2)連接OB(O是坐標原點),若△BOC的面積為3,求該一次函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 的圖象與x軸交于A、B兩點(點A在點B的左邊),與y軸交于點C,點D為拋物線的頂點.點A坐標的為
的圖象與x軸交于A、B兩點(點A在點B的左邊),與y軸交于點C,點D為拋物線的頂點.點A坐標的為![]() ,點C的坐標為
,點C的坐標為![]() .
.
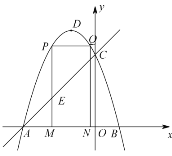
(Ⅰ)求拋物線的解析式;
(Ⅱ)點M為線段![]() 上一點(點M不與點A、B重合),過點M作i軸的垂線,與直線
上一點(點M不與點A、B重合),過點M作i軸的垂線,與直線![]() 交于點E,與拋物線交于點P,過點P作
交于點E,與拋物線交于點P,過點P作![]() 交拋物線于點Q,過點Q作
交拋物線于點Q,過點Q作![]() 軸于點N.若點P在點Q左邊,當矩形
軸于點N.若點P在點Q左邊,當矩形![]() 的周長最大時,求
的周長最大時,求![]() 的面積;
的面積;
(Ⅲ)在(Ⅱ)的條件下,當矩形![]() 的周長最大時,連接
的周長最大時,連接![]() ,過拋物線上一點F作y軸的平行線,與直線
,過拋物線上一點F作y軸的平行線,與直線![]() 交于點G(點G在點F的上方).若
交于點G(點G在點F的上方).若![]() ,求點F的坐標.
,求點F的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com