
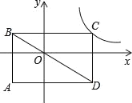
【題目】如圖,矩形ABCD的對(duì)角線BD經(jīng)過(guò)坐標(biāo)原點(diǎn),矩形的邊分別平行于坐標(biāo)軸,點(diǎn)C在反比例函數(shù)![]() 的圖象上.若點(diǎn)A的坐標(biāo)為(﹣4,﹣4),則k的值為( )
的圖象上.若點(diǎn)A的坐標(biāo)為(﹣4,﹣4),則k的值為( )
A. 16B. ﹣3C. 5D. 5或﹣3
【答案】C
【解析】
先利用矩形的性質(zhì)得到矩形AEOF的面積等于矩形OMCN的面積,則根據(jù)反比例函數(shù)圖象上點(diǎn)的坐標(biāo)特征得到|k2﹣2k+1|=4×4,然后解關(guān)于k的一元二次方程即可.
設(shè)C(x,y),
如圖,∵矩形ABCD的對(duì)角線BD經(jīng)過(guò)坐標(biāo)原點(diǎn),矩形的邊分別平行于坐標(biāo)軸,
∴△ABD和△CDB的面積相等,
∴矩形AEOF的面積等于矩形OMCN的面積,
∴xy=k2﹣2k+1=4×4,
即(k﹣1)2=16,
解得k1=﹣3,k2=5,
∵C點(diǎn)在第一象限,
∴k=5,
故選C.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】隨著通訊技術(shù)的迅猛發(fā)展,人與人之間的溝通方式更多樣、便捷.某校數(shù)學(xué)興趣小組設(shè)計(jì)了“你最喜歡的溝通方式”調(diào)查問(wèn)卷(每人必選且只選一種),在全校范圍內(nèi)隨機(jī)調(diào)查了部分學(xué)生,將統(tǒng)計(jì)結(jié)果繪制了如下兩幅不完整的統(tǒng)計(jì)圖,請(qǐng)結(jié)合圖中所給的信息解答下列問(wèn)題:
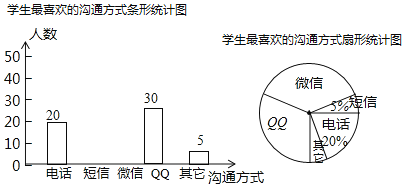
(1)這次統(tǒng)計(jì)共抽查了 名學(xué)生;在扇形統(tǒng)計(jì)圖中,表示“QQ”的扇形圓心角的度數(shù)為 ;
(2)將條形統(tǒng)計(jì)圖補(bǔ)充完整;
(3)該校共有1500名學(xué)生,請(qǐng)估計(jì)該校最喜歡用“微信”進(jìn)行溝通的學(xué)生有多少名?
(4)某天甲、乙兩名同學(xué)都想從“微信”、“QQ”、“電話”三種溝通方式中選一種方式與對(duì)方聯(lián)系,請(qǐng)用列表或畫樹狀圖的方法求出甲、乙兩名同學(xué)恰好選擇同一種溝通方式的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,菱形ABCD位于平面直角坐標(biāo)系中,拋物線y=ax2+bx+c經(jīng)過(guò)菱形的三個(gè)頂點(diǎn)A、B、C,已知A(﹣3,0)、B(0,﹣4).
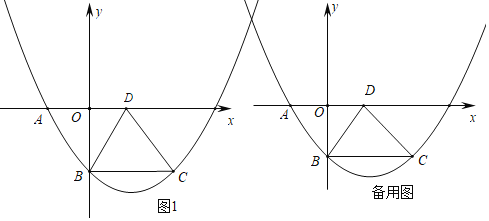
(1)求拋物線解析式;
(2)線段BD上有一動(dòng)點(diǎn)E,過(guò)點(diǎn)E作y軸的平行線,交BC于點(diǎn)F,若S△BOD=4S△EBF,求點(diǎn)E的坐標(biāo);
(3)拋物線的對(duì)稱軸上是否存在點(diǎn)P,使△BPD是以BD為斜邊的直角三角形?如果存在,求出點(diǎn)P的坐標(biāo);如果不存在,說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系中B(﹣1,0),A(0,m),m>0,將線段AB線繞B點(diǎn)逆時(shí)針旋轉(zhuǎn)90°得BC,AC的中點(diǎn)為D點(diǎn).
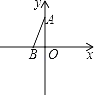
(1)m=2時(shí),畫圖并直接寫出D點(diǎn)的坐標(biāo) ;
(2)若雙曲線![]() (x<0)過(guò)C,D兩點(diǎn),求反比例的解析式;
(x<0)過(guò)C,D兩點(diǎn),求反比例的解析式;
(3)在(2)的條件下,點(diǎn)P在C點(diǎn)左側(cè),且在雙曲線上,以CP為邊長(zhǎng)畫正方形CPEF,且點(diǎn)E在x軸上,求P點(diǎn)坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:如圖,平行四邊形ABCD,對(duì)角線AC與BD相交于點(diǎn)E,點(diǎn)G為AD的中點(diǎn),連接CG,CG的延長(zhǎng)線交BA的延長(zhǎng)線于點(diǎn)F,連接FD.
(1)求證:AB=AF;
(2)若AG=AB,∠BCD=120°,判斷四邊形ACDF的形狀,并證明你的結(jié)論.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,矩形ABCD的邊長(zhǎng)AD=6,AB=4,E為AB的中點(diǎn),F在邊BC上,且BF=2FC,AF分別與DE、DB相交于點(diǎn)M、N,則MN的長(zhǎng)為_____.
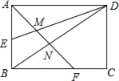
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】把兩個(gè)全等的矩形ABCD和EFGH如圖1擺放(點(diǎn)D和點(diǎn)G重合,點(diǎn)C和點(diǎn)H重合),點(diǎn)A、D(G)在同一條直線上,AB=6cm,BC=8cm.如圖2,△ABC從圖1位置出發(fā),沿BC方向勻速運(yùn)動(dòng),速度為1cm/s,AC與GH交于點(diǎn)P;同時(shí),點(diǎn)Q從點(diǎn)E出發(fā),沿EF方向勻速運(yùn)動(dòng),速度為1cm/s.點(diǎn)Q停止運(yùn)動(dòng)時(shí),△ABC也停止運(yùn)動(dòng).設(shè)運(yùn)動(dòng)時(shí)間為t(s)(0<t<6).
(1)當(dāng)t為何值時(shí),CQ∥FH;
(2)過(guò)點(diǎn)Q作QM⊥FH于點(diǎn)N,交GF于點(diǎn)M,設(shè)五邊形GBCQM的面積為y(cm2),求y與t之間的函數(shù)關(guān)系式;
(3)在(2)的條件下,是否存在某一時(shí)刻,使點(diǎn)M在線段PC的中垂線上?若存在,請(qǐng)求出t的值;若不存在,請(qǐng)說(shuō)明理由.
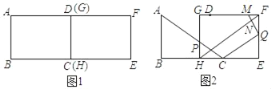
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖①,等腰Rt△ABC中,∠C=90o,D是AB的中點(diǎn),Rt△DEF的兩條直角邊DE、DF分別與AC、BC相交于點(diǎn)M、N.
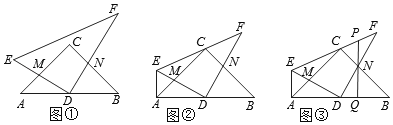
(1)思考推證:CM+CN=BC;
(2)探究證明:如圖②,若EF經(jīng)過(guò)點(diǎn)C,AE⊥AB,判斷線段MA、ME、MC、DN四條線段之間的數(shù)量關(guān)系,并證明你的結(jié)論;
(3)拓展應(yīng)用:如圖③,在②的條件下,若AB=4,AE=1,Q為線段DB上一點(diǎn),DQ=![]() ,QN的延長(zhǎng)線交EF于點(diǎn)P,求線段PQ的長(zhǎng).
,QN的延長(zhǎng)線交EF于點(diǎn)P,求線段PQ的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
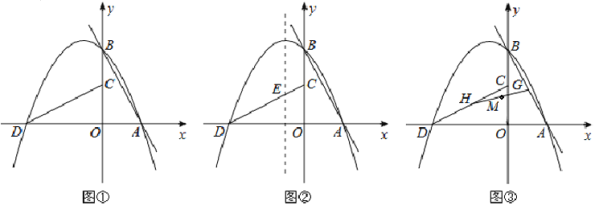
【題目】如圖①,定義:直線![]() (m<0, n>0) 與x、y軸分別相交于A、B兩點(diǎn),將△AOB繞著點(diǎn)O逆時(shí)針旋轉(zhuǎn)90°得到△COD,過(guò)點(diǎn)A、B、D的拋物線P叫做直線l的“糾纏拋物線”,反之,直線l叫做P的“糾纏直線”,兩線“互為糾纏線”。
(m<0, n>0) 與x、y軸分別相交于A、B兩點(diǎn),將△AOB繞著點(diǎn)O逆時(shí)針旋轉(zhuǎn)90°得到△COD,過(guò)點(diǎn)A、B、D的拋物線P叫做直線l的“糾纏拋物線”,反之,直線l叫做P的“糾纏直線”,兩線“互為糾纏線”。
(1) 若![]() ,則糾纏拋物線P的函數(shù)解析式是 .
,則糾纏拋物線P的函數(shù)解析式是 .
(2) 判斷并說(shuō)明![]() 與
與![]() 是否“互為糾纏線”.
是否“互為糾纏線”.
(3) 如圖②,若糾纏直線![]() ,糾纏拋物線P的對(duì)稱軸與CD相交于點(diǎn)E,點(diǎn)F在l上,點(diǎn)Q在P的對(duì)稱軸上,當(dāng)以點(diǎn)C、E、Q、F為頂點(diǎn)的四邊形是以CE為一邊的平行四邊形時(shí),求點(diǎn)Q的坐標(biāo).
,糾纏拋物線P的對(duì)稱軸與CD相交于點(diǎn)E,點(diǎn)F在l上,點(diǎn)Q在P的對(duì)稱軸上,當(dāng)以點(diǎn)C、E、Q、F為頂點(diǎn)的四邊形是以CE為一邊的平行四邊形時(shí),求點(diǎn)Q的坐標(biāo).
(4) 如圖③,在(3)的條件下,G為線段AB上的一個(gè)動(dòng)點(diǎn),G點(diǎn)隨著△AOB旋轉(zhuǎn)到線段CD上的H點(diǎn),連接H、G,取HG的中點(diǎn)M,當(dāng)點(diǎn)G從A開始運(yùn)動(dòng)到B點(diǎn),直接寫出點(diǎn)M的運(yùn)動(dòng)路徑長(zhǎng)。
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com