
【題目】如圖,拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=1,與x軸的一個交點坐標為(-1,0),其部分圖象如圖所示,下列結論:
①4ac<b2;
②方程ax2+bx+c=0的兩個根是x1=-1,x2=3;
③3a+c>0;
④當y<0時,x的取值范圍是-1≤x<3;
⑤當x<0時,y隨x增大而增大。
其中結論正確的個數是( )
A.4個
B.3個
C.2個
D.1個
【答案】B
【解析】解:①由拋物線圖象與x軸有兩個不同的交點可得,判別式b2-4ac>0,即4ac<b2 , 故①正確;
②因為拋物線的對稱軸為直線x=1,且與x軸交于一點(-1,0),則另一點為(3,0),故方程ax2+bx+c=0的兩個根是x1=-1,x2=3,故②正確;
③由對稱軸 ![]() ,可得b=-2a,即拋物線y=ax2-2ax+c,由拋物線經過(-1,0)代入,則a+2a+c=0,即3a+c=0,故③錯誤;
,可得b=-2a,即拋物線y=ax2-2ax+c,由拋物線經過(-1,0)代入,則a+2a+c=0,即3a+c=0,故③錯誤;
④當y<0時,拋物線的圖象應該在x軸的下方,則x的取值范圍是x<-1或x>3,故④錯誤;
⑤當x<0時,y隨x增大而增大,故⑤正確。
故選B.
【考點精析】本題主要考查了二次函數的圖象和二次函數的性質的相關知識點,需要掌握二次函數圖像關鍵點:1、開口方向2、對稱軸 3、頂點 4、與x軸交點 5、與y軸交點;增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】如圖1,在正方形ABCD中,點E,F分別是邊BC,AB上的點,且CE=BF.連接DE,過點E作EG⊥DE,使EG=DE,連接FG,FC.
(1)請判斷:FG與CE的數量關系是 , 位置關系是;
(2)如圖2,若點E,F分別是邊CB,BA延長線上的點,其它條件不變,(1)中結論是否仍然成立?請作出判斷并給予證明;
(3)如圖3,若點E,F分別是邊BC,AB延長線上的點,其它條件不變,(1)中結論是否仍然成立?請直接寫出你的判斷.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了響應“足球進校園”的目標,某校計劃為學校足球隊購買一批足球,已知購買2個A品牌的足球和3個B品牌的足球共需380元;購買4個A品牌的足球和2個B品牌的足球共需360元.
(1)求A,B兩種品牌的足球的單價.
(2)求該校購買20個A品牌的足球和2個B品牌的足球的總費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為保障我國海外維和部隊官兵的生活,現需通過A港口、B港口分別運送100噸和50噸生活物資.已知該物資在甲倉庫存有80噸,乙倉庫存有70噸,若從甲、乙兩倉庫運送物資到港口的費用(元/噸)如表所示:
港口 | 運費(元/臺) | |
甲庫 | 乙庫 | |
A港 | 14 | 20 |
B港 | 10 | 8 |
(1)設從甲倉庫運送到A港口的物資為x噸,求總運費y(元)與x(噸)之間的函數關系式,并寫出x的取值范圍;
(2)求出最低費用,并說明費用最低時的調配方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A是雙曲線y= ![]() 在第三象限分支上的一個動點,連結AO并延長交另一分支于點B,以AB為邊作等邊三角形ABC,點C在第四象限內,且隨著點A的運動,點C的位置也在不斷變化,但點C始終在雙曲線y=
在第三象限分支上的一個動點,連結AO并延長交另一分支于點B,以AB為邊作等邊三角形ABC,點C在第四象限內,且隨著點A的運動,點C的位置也在不斷變化,但點C始終在雙曲線y= ![]() 上運動,則k的值是.
上運動,則k的值是.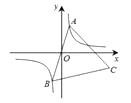
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD的邊長為2cm,∠A=60°. ![]() 是以點A為圓心、AB長為半徑的弧,
是以點A為圓心、AB長為半徑的弧, ![]() 是以點B為圓心、BC長為半徑的弧.則陰影部分的面積為cm2 .
是以點B為圓心、BC長為半徑的弧.則陰影部分的面積為cm2 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】
(1)如圖1,在△ABC中,BA=BC,D,E是AC邊上的兩點,且滿足∠DBE= ![]() ∠ABC(0°<∠CBE<∠
∠ABC(0°<∠CBE<∠ ![]() ABC).以點B為旋轉中心,將△BEC按逆時針旋轉∠ABC,得到△BE′A(點C與點A重合,點E到點E′處)連接DE′, 求證:DE′=DE.
ABC).以點B為旋轉中心,將△BEC按逆時針旋轉∠ABC,得到△BE′A(點C與點A重合,點E到點E′處)連接DE′, 求證:DE′=DE.
(2)如圖2,在△ABC中,BA=BC,∠ABC=90°,D,E是AC邊上的兩點,且滿足∠DBE= ![]() ∠ABC(0°<∠CBE<45°). 求證:DE2=AD2+EC2 .
∠ABC(0°<∠CBE<45°). 求證:DE2=AD2+EC2 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】據悉,2013年財政部核定海南省發行的60億地方政府“債券資金”,全部用于交通等重大項目建設.以下是60億“債券資金”分配統計圖: 
(1)請將條形統計圖補充完整;
(2)在扇形統計圖中,a= , b=(都精確到0.1);
(3)在扇形統計圖中,“教育文化”對應的扇形圓心角的度數為°(精確到1°)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com