
 如圖,在矩形ABCD中,AB=8,BC=12,點E是BC的中點,連接AE,將△ABE沿AE折疊,點B落在點F處,連接FC,則sin∠ECF=$\frac{4}{5}$.
如圖,在矩形ABCD中,AB=8,BC=12,點E是BC的中點,連接AE,將△ABE沿AE折疊,點B落在點F處,連接FC,則sin∠ECF=$\frac{4}{5}$. 分析 過E作EH⊥CF于H,由折疊的性質得BE=EF,∠BEA=∠FEA,由點E是BC的中點,得到CE=BE,得到△EFC是等腰三角形,根據等腰三角形的性質得到∠FEH=∠CEH,推出△ABE∽△EHC,求得EH=$\frac{24}{5}$,即可得出sin∠ECF的值.
解答 解:過E作EH⊥CF于H,
由折疊的性質得: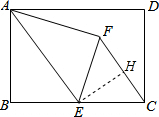 BE=EF,∠BEA=∠FEA,
BE=EF,∠BEA=∠FEA,
∵點E是BC的中點,
∴CE=BE,
∴EF=CE,
∴∠FEH=∠CEH,
∴∠AEB+∠CEH=90°,
在矩形ABCD中,
∵∠B=90°,
∴∠BAE+∠BEA=90°,
∴∠BAE=∠CEH,∠B=∠EHC,
∴△ABE∽△EHC,
∴$\frac{AB}{EH}=\frac{AE}{CE}$,
∵AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=10,
∴EH=$\frac{24}{5}$,
∴sin∠ECF=sin∠ECH=$\frac{AB}{AE}$=$\frac{4}{5}$,
故答案為:$\frac{4}{5}$.
點評 本題考查了折疊問題:折疊前后兩圖形全等,即對應線段相等;對應角相等.也考查了矩形的性質以及勾股定理.


科目:初中數學 來源: 題型:解答題
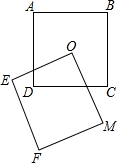 正方形ABCD與正方形OEFM的邊長都等于1,且O點是正方形ABCD的對角線交點,現將正方形OEFM繞O點旋轉,探究在旋轉過程中兩個正方形重疊部分的面積是否發生變化,為什么?如果沒變化.那么面積是多少?
正方形ABCD與正方形OEFM的邊長都等于1,且O點是正方形ABCD的對角線交點,現將正方形OEFM繞O點旋轉,探究在旋轉過程中兩個正方形重疊部分的面積是否發生變化,為什么?如果沒變化.那么面積是多少?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,一次函數y=ax+b的圖象與反比例函數的圖象交于A(-4,2),B(2,n)兩點,且與x軸交于點C.
如圖,一次函數y=ax+b的圖象與反比例函數的圖象交于A(-4,2),B(2,n)兩點,且與x軸交于點C.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
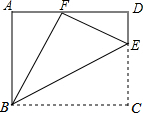 如圖,矩形ABCD中,點E是CD邊長的一點,△BCE沿BE折疊為△BFE,點F在AD上.
如圖,矩形ABCD中,點E是CD邊長的一點,△BCE沿BE折疊為△BFE,點F在AD上.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 200名學生是總體 | B. | 200名學生是一個樣本 | ||
| C. | 每個學生是個體 | D. | 全縣七年級學生的體重是總體 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com