
這是一個著名定理的一種說理過程:將四個如圖1所示的直角三角形經過平移、旋轉、對稱變換運動,拼成如圖2所示的中空的四邊形ABCD.
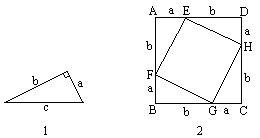
(1)請說明:四邊形ABCD和EFGH都是正方形;
(2)結合圖形說明等式a2+b2=c2成立,并用適當的文字敘述這個定理的結論.
|
解:(1)在四邊形ABCD中,有∠A=∠B=∠C=∠D= 在四邊形EFGH中,有EF=FG=GH=HE=c,∠HEF= (2)在如圖中,由于正方形ABCD的面積-4個直角三角形的面積=正方形EFGH的面積因此(a+b)2-4× 即:a2+2ab+b2-2ab=c2 所以:a2+b2=c2 這個定理的結論是:直角三角形中,兩條直角邊長的平方的和等于斜邊長的平方. |
|
思路與技巧:(1)關鍵是要說明四邊形ABCD和EFGH的四條邊相等,四個角都是直角;(2)關鍵是從面積關系入手,尋找字母a、b、c之間的關系. 評注:著名定理本身的推導方法并不復雜,只要我們認真學好數學基礎知識,注意培養自己的創新思維能力,也許會從中受到一些啟發,有所發明創造. |


 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:初中數學 來源: 題型:
| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
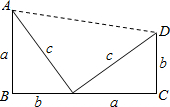 (2010•南潯區模擬)利用圖中圖形的有關面積的等量關系都能證明數學中一個十分著名的定理,此證明方法就是美國第二十任總統伽菲爾德最先完成的,人們為了紀念他,把這一證法稱為“總統”證法.這個定理稱為
(2010•南潯區模擬)利用圖中圖形的有關面積的等量關系都能證明數學中一個十分著名的定理,此證明方法就是美國第二十任總統伽菲爾德最先完成的,人們為了紀念他,把這一證法稱為“總統”證法.這個定理稱為查看答案和解析>>
科目:初中數學 來源: 題型:
 在我們的生活中處處有數學的身影,請看圖,折疊一張三角形紙片,把三角形的三個角拼在一起,就得到一個著名的幾何定理,請你寫出這一定理
在我們的生活中處處有數學的身影,請看圖,折疊一張三角形紙片,把三角形的三個角拼在一起,就得到一個著名的幾何定理,請你寫出這一定理查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com