【答案】
分析:(1)原式第一項利用負指數公式化簡,第二項利用零指數公式化簡,第三項利用絕對值的代數意義化簡,最后一項化為最簡二次根式,合并即可得到結果;
(2)原式第一項利用乘法分配律化簡,第二項化為最簡二次根式,合并同類二次根式即可得到結果;
(3)方程左邊的多項式利用十字相乘法分解因式,然后利用兩數相乘積為0,兩因式中至少有一個為0轉化為兩個一元一次方程,求出一次方程的解即可得到原方程的解;
(4)將方程整理為一般形式,找出a,b及c的值,計算出根的判別式的值大于0,代入求根公式即可求出解.
解答:解:(1)原式=6-1+2-
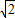
+3
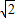
=7+2

;
(2)原式=6

-6
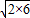
-8
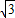
=3-12
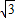
-8

=3-20
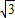
;
(3)x
2+4x-5=0,
分解因式得:(x-1)(x+5)=0,
可得x-1=0或x+5=0,
解得:x
1=1,x
2=-5;
(4)x(2x+2)=4x+6,
整理得:x
2-x-3=0,
這里a=1,b=-1,c=-1,
∵△=1+4=5,
∴x=
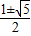
,
則x
1=
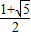
,x
2=

.
點評:此題考查了解一元二次方程-因式分解法,利用此方法解方程時,首先將方程右邊化為0,左邊化為積的形式,然后利用兩數相乘積為0,兩因式中至少有一個為0轉化為兩個一元一次方程來求解.


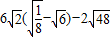
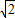 +3
+3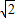 =7+2
=7+2 ;
; -6
-6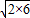 -8
-8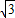 =3-12
=3-12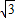 -8
-8 =3-20
=3-20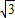 ;
;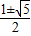 ,
,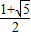 ,x2=
,x2= .
.

