
分析 代數式$\frac{3+x}{2}$-1的值不大于$\frac{4x+3}{6}$的值,則可以列不等式$\frac{3+x}{2}$-1≤$\frac{4x+3}{6}$,解不等式即可求解.
解答 解:根據題意得:$\frac{3+x}{2}$-1≤$\frac{4x+3}{6}$,
去分母,得3(3+x)-6≤4x+3,
去括號,得9+3x-6≤4x+3,
移項,得3x-4x≤3-9+6,
合并同類項,得-x≤0,
系數化成1得x≥0.
點評 本題考查了不等式的解法,基本操作方法與解一元一次方程基本相同,都有如下步驟:①去分母;②去括號;③移項;④合并同類項;⑤化系數為1.以上步驟中,只有①去分母和⑤化系數為1可能用到性質3,即可能變不等號方向,其他都不會改變不等號方向.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
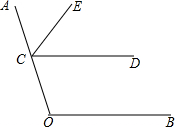 如圖,點C在射線OA上,CE平分∠ACD.OF平分∠COB并與射線CD交于點F.
如圖,點C在射線OA上,CE平分∠ACD.OF平分∠COB并與射線CD交于點F.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com