【題目】在下圖中，C，D是線段AB上的兩點，已知BC＝
AB，AD＝
AB，AB＝12 cm，求CD，BD的長．
【答案】CD＝5cm，BD＝8cm．
【解析】試題分析：首先根據AB、BC和AD的關系求出BC和AD的長度，然后根據CD=AB-AD-BC以及BD=DC+BC求出線段的長度．
試題解析：∵AB=12cm， ∴BC=
AB=
×12=3cm，AD=
AB=
×12=4cm，
∴CD=AB-AD-BC=12-4-3=5cm，BD=DC+BC=5+3=8cm．
試題分析：本題主要考查的就是線段長度的計算以及線段之間的關系，屬于簡單題型．本題中已經給出圖形，我們只需要按照圖形解答即可，在解決線段長度問題的時候，有時候沒有圖形，我們首先要根據點的位置畫出圖形，然后根據線段之間的關系來進行求解，畫圖是解決這類問題的首要條件．
浙江名校名師金卷系列答案科目：初中數學 來源： 題型：
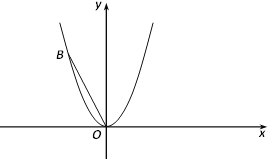
【題目】如圖，平面直角坐標系xOy中，拋物線
經過點B(－2，4)．
（1）求a的值；
（2）作Rt△OAB，使∠BOA＝90°，且OB＝2OA，求點A坐標；
（3）在（2）的條件下，過點A作直線AC⊥x軸于點C，交拋物線于點D，將該拋物線向左或向右平移t（t＞0）個單位長度，記平移后點D的對應點為D′，點B的對應點為B′．當CD′＋OB′的值最小時，請直接寫出t的值和平移后相應的拋物線解析式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】圖a、圖b是兩張形狀、大小完全相同的方格紙，方格紙中每個小正方形的邊長為1，點A、B、D在小正方形的頂點上．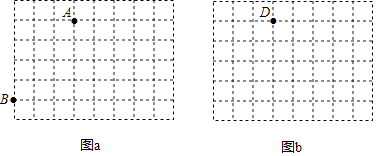 
（1）在圖a中畫出△ABC（點C在小正方形頂點上），使△ABC是等腰三角形，且∠ABC=45°；
（2）在圖b中畫出△DEF（E、F在小正方形頂點上），使△DEF∽ABC且相似比為1： 
．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知二次函數y1=x2+mx+n的圖象經過點P（﹣3，1），對稱軸是經過（﹣1，0）且平行于y軸的直線．
（1）求m，n的值．
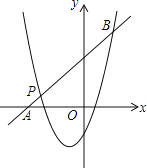
（2）如圖，一次函數y2=kx+b的圖象經過點P，與x軸相交于點A，與二次函數的圖象相交于另一點B，點B在點P的右側，PA：PB=1：5，求一次函數的表達式．
（3）直接寫出y1＞y2時x的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了調查瑞州市2016年初三年級學生的身高，從中抽取出200名學生進行調查，這個問題中樣本容量為( )
A. 被抽取的200名學生的身高 B. 200
C. 200名 D. 初三年級學生的身高
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com