
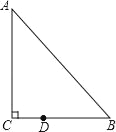
【題目】如圖,在Rt△ABC中,∠C=90°,∠B=40°,點D在邊BC上,BD=2CD,把△ABC繞點D逆時針旋轉m(0<m<180)度后,如果點B恰好落在初始Rt△ABC的邊上,則m=_____.
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
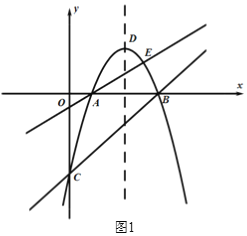
【題目】如圖1,拋物線![]() 與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C,直線AE:
與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C,直線AE:![]() 與拋物線相交于另一點E,點D為拋物線的頂點.
與拋物線相交于另一點E,點D為拋物線的頂點.
(1)求直線BC的解析式及點E的坐標;
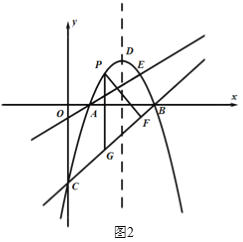
(2)如圖2,直線AE上方的拋物線上有一點P,過點P作PF⊥BC于點F,過點P作平行于![]() 軸的直線交直線BC于點G,當△PFG周長最大時,在
軸的直線交直線BC于點G,當△PFG周長最大時,在![]() 軸上找一點M,在AE上找一點N,使得
軸上找一點M,在AE上找一點N,使得![]() 值最小,請求出此時N點的坐標及
值最小,請求出此時N點的坐標及![]() 的最小值;
的最小值;
(3)在第(2)問的條件下,點R為拋物線對稱軸上的一點,在平面直角坐標系中是否存在點S,使以點N,E,R,S為頂點的四邊形為矩形,若存在,請直接寫出點S的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于點P,點P在第一象限.PA⊥x軸于點A,PB⊥y軸于點B.一次函數的圖象分別交
的圖象交于點P,點P在第一象限.PA⊥x軸于點A,PB⊥y軸于點B.一次函數的圖象分別交![]() 軸、
軸、![]() 軸于點C、D,且S△PBD=4,
軸于點C、D,且S△PBD=4, ![]() .
.

(1)求點D的坐標;
(2)求一次函數與反比例函數的解析式;
(3)根據圖象寫出當![]() 時,一次函數的值大于反比例函數的值的
時,一次函數的值大于反比例函數的值的![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),已知點G在正方形ABCD的對角線AC上,GE⊥BC,垂足為點E,GF⊥CD,垂足為點F.
(1)證明與推斷:
①求證:四邊形CEGF是正方形;
②推斷:![]() 的值為 :
的值為 :
(2)探究與證明:
將正方形CEGF繞點C順時針方向旋轉α角(0°<α<45°),如圖(2)所示,試探究線段AG與BE之間的數量關系,并說明理由:
(3)拓展與運用:
正方形CEGF在旋轉過程中,當B,E,F三點在一條直線上時,如圖(3)所示,延長CG交AD于點H.若AG=6,GH=2![]() ,則BC= .
,則BC= .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】端午節“賽龍舟,吃粽子”是中華民族的傳統習俗.節日期間,小邱家包了三種不同餡的粽子,分別是:紅棗粽子(記為A),豆沙粽子(記為B),肉粽子(記為C),這些粽子除了餡不同,其余均相同.粽子煮好后,小邱的媽媽給一個白盤中放入了兩個紅棗粽子,一個豆沙粽子和一個肉粽子;給一個花盤中放入了兩個肉粽子,一個紅棗粽子和一個豆沙粽子.
根據以上情況,請你回答下列問題:
(1)假設小邱從白盤中隨機取一個粽子,恰好取到紅棗粽子的概率是多少?
(2)若小邱先從白盤里的四個粽子中隨機取一個粽子,再從花盤里的四個粽子中隨機取一個粽子,請用列表法或畫樹狀圖的方法,求小邱取到的兩個粽子中一個是紅棗粽子、一個是豆沙粽子的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,點D在BC上,BD=DC,過點D作DE⊥AC,垂足為E,⊙O經過A,B,D三點.
(1)求證:AB是⊙O的直徑;
(2)判斷DE與⊙O的位置關系,并加以證明;
(3)若⊙O的半徑為3,∠BAC=60°,求DE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
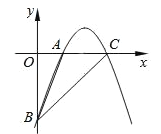
【題目】已知二次函數y=﹣x2+bx+c(b,c均為常數)的圖象經過兩點A(2,0),B(0,﹣6).
(1)求這個二次函數的解析式;
(2)若點C(m,0)(m>2)在這個二次函數的圖象上,連接AB,BC,求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】基本事實:“若ab=0,則a=0或b=0”.一元二次方程x2-x-2=0可通過因式分解化為(x-2)(x+1)=0,由基本事實得x-2=0或x+1=0,即方程的解為x=2或x=-1.
(1)、試利用上述基本事實,解方程:2x2-x=0:
(2)、若(x2+y2)(x2+y2-1)-2=0,求x2+y2的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等腰RtABC中,![]() ,點P在以斜邊AB為直徑的半圓上,M為PC的中點.當點P沿半圓從點A運動至點B時,點M運動的路徑長是( )
,點P在以斜邊AB為直徑的半圓上,M為PC的中點.當點P沿半圓從點A運動至點B時,點M運動的路徑長是( )
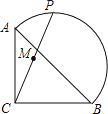
A. ![]() B. 2
B. 2![]() C.
C. ![]() D. 4
D. 4![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com