【題目】如圖①，若BC是Rt△ABC和Rt△DBC的公共斜邊，則A、B、C、D在以BC為直徑的圓上，則叫它們“四點共圓”．如圖②，△ABC的三條高AD、BE、CF相交于點H，則圖②中“四點共圓”的組數為（ ）
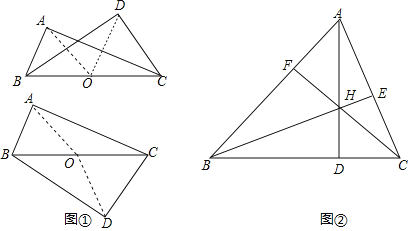
A.2B.3C.4D.6
科目：初中數學 來源： 題型：
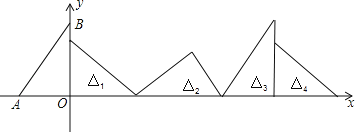
【題目】如圖，在直角坐標系中，已知點A（﹣3，0），B（0，4），對△OAB連續作旋轉變換，依次得到△1、△2、△3、△4…，則△2020的直角頂點的坐標為_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面坐標系xOy中，點A的坐標為（1，0），點P的橫坐標為2，將點A繞點P旋轉，使它的對應點B恰好落在x軸上（不與A點重合）；再將點B繞點O逆時針旋轉90°得到點C．
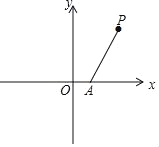
（1）直接寫出點B和點C的坐標；
（2）求經過A，B，C三點的拋物線的表達式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在一張矩形紙片
中，
，
，現將這張紙片按下列圖示方法折疊，請解決下列問題：
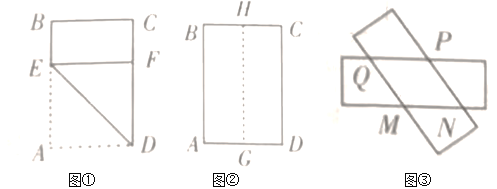
（1）如圖①，折痕為
，點
的對應點
在
上，求證：四邊形
是正方形；
（2）如圖②，
、
分別為
、
的中點，把矩形紙片沿著
剪開，變成兩張矩形紙片，將兩張紙片任意疊合后（如圖③），判斷重疊四邊形
的形狀，并證明；
（3）在（2）中，重疊四邊形的周長是否存在最大值或最小值？若存在，請求出最大值或最小值；若不存在，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
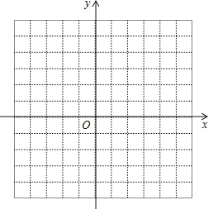
【題目】已知：二次函數y＝x2﹣mx+
m+1(m為常數).若這個二次函數的圖象與x軸只有一個公共點A，且A點在x軸的正半軸上.
(1)求m的值.
(2)四邊形AOBC是正方形，且點B在y軸的負半軸上，現將這個二次函數的圖象平移，使平移后的函數圖象恰好經過B，C兩點，求平移后的圖象對應的函數解析式.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知⊙O半徑為1，若點P在⊙O外且⊙O上存在點A、B使得∠APB＝60°，則稱點P是⊙O的領域點．
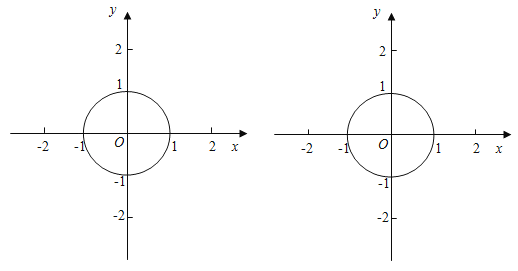
（1）對以下情況，用三角板或量角器嘗試畫圖，并判斷點P是否是⊙O的領域點（在橫線上填“是”或“不是”）．
①當OP＝1.2時， 點P ⊙O的領域點
| ②當OP＝2時， 點P ⊙O的領域點
| ③當OP＝3時， 點P ⊙O的領域點
|
（2）若點P是⊙O的領域點，則OP的取值范圍是 ；
（3）如圖，以圓心O為坐標原點建立平面直角坐標系xOy，設直線y＝﹣x+b（b＞0）與x軸、y軸分別相交于點M、N．
①若線段MN上有且只有一個點是⊙O的領域點，求b的值；
②若線段MN上存在⊙O的領域點，求b的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
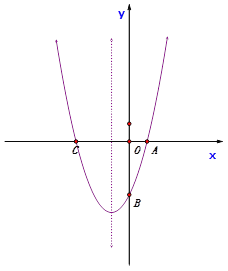
【題目】如圖，已知拋物線
經過點A（1,0）和點B （0，-3），與x軸交于另一點C。
（1）求拋物線的解析式。
（2）在拋物線上是否存在一點D，使△ACD的面積與△ABC的面積相等（點D不與點B重合）？若存在，求出點D的坐標；若不存在，請說明理由。
（3）若點P是拋物線上的動點，點Q是拋物線對稱軸上的動點，那么是否存在這樣的點P，使以點A、C、P、Q為頂點的四邊形為平行四邊形？若存在，求出點P的坐標；若不存在，請說明理由。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，點
為坐標原點，拋物線
經過點
和
.
（1）求該拋物線的解析式及頂點坐標；
（2）把該拋物線向 （填“上”或“下”）平移 個單位長度，得到的拋物線與
軸只有一個公共點；
（3）平移該拋物線，使平移后的拋物線經過點
，且與
軸交于點
，同時滿足以
，，為頂點的三角形是等腰直角三角形，請你寫出平移過程，并說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知二次函數y＝x2＋bx＋c的圖象過點A（1，m），B（3，m），若點M（－2，y1），N（－1，y2），K（8，y3）也在二次函數y＝x2＋bx＋c的圖象上，將y1，y2，y3按從小到大的順序用“＜”連接，結果是___________________．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
