
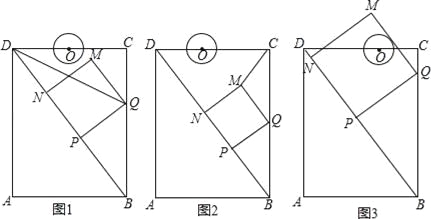
【題目】如圖,在矩形ABCD中,AB=6cm,AD=8cm,點P從點B出發,沿對角線BD向點D勻速運動,速度為4cm/s,過點P作PQ⊥BD交BC于點Q,以PQ為一邊作正方形PQMN,使得點N落在射線PD上,點O從點D出發,沿DC向點C勻速運動,速度為3m/s,以O為圓心,0.8cm為半徑作⊙O,點P與點O同時出發,設它們的運動時間為t(單位:s)(0<t<![]() ).
).
(1)如圖1,連接DQ平分∠BDC時,t的值為 ;
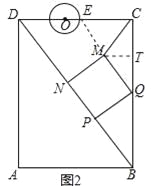
(2)如圖2,連接CM,若△CMQ是以CQ為底的等腰三角形,求t的值;
(3)請你繼續進行探究,并解答下列問題:
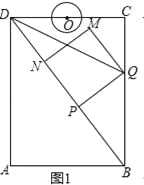
①證明:在運動過程中,點O始終在QM所在直線的左側;
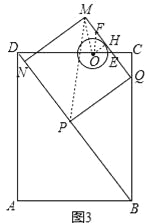
②如圖3,在運動過程中,當QM與⊙O相切時,求t的值;并判斷此時PM與⊙O是否也相切?說明理由.
【答案】見解析
【解析】試題分析:本題考查圓綜合題、正方形的性質、相似三角形的判定和性質、切線的判定和性質、勾股定理、角平分線的性質等知識,利用相似三角形的性質構建方程,最后一個問題利用反證法證明解題.
(1)先利用△PBQ∽△CBD求出PQ、BQ,再根據角平分線性質,列出方程解決問題.
(2)由△QTM∽△BCD,得![]() 列出方程即可解決.
列出方程即可解決.
(3)①如圖2中,由此QM交CD于E,求出DE、DO利用差值比較即可解決問題.
②如圖3中,由①可知⊙O只有在左側與直線QM相切于點H,QM與CD交于點E.由△OHE∽△BCD,得![]() ,列出方程即可解決問題.利用反證法證明直線PM不可能由⊙O相切.
,列出方程即可解決問題.利用反證法證明直線PM不可能由⊙O相切.
(1)解:如圖1中,∵四邊形ABCD是矩形,
∴∠A=∠C=∠ADC=∠ABC=90°,AB=CD=6.AD=BC=8,
∴![]() ,
,
∵PQ⊥BD,
∴∠BPQ=90°=∠C,
∵∠PBQ=∠DBC,
∴△PBQ∽△CBD,
∴![]() ,
,
∴![]() ,
,
∴PQ=3t,BQ=5t,
∵DQ平分∠BDC,QP⊥DB,QC⊥DC,
∴QP=QC,
∴3t=8-5t,
∴t=1,
故答案為:1.
(2)解:如圖2中,作MT⊥BC于T.
∵MC=MQ,MT⊥CQ,
∴TC=TQ,
由(1)可知TQ=![]() (8-5t),QM=3t,
(8-5t),QM=3t,
∵MQ∥BD,
∴∠MQT=∠DBC,
∵∠MTQ=∠BCD=90°,
∴△QTM∽△BCD,
∴![]() ,
,
∴![]() ,
,
∴t=![]() (s),
(s),
∴t=![]() s時,△CMQ是以CQ為底的等腰三角形.
s時,△CMQ是以CQ為底的等腰三角形.
(3)①證明:如圖2中,由此QM交CD于E,
∵EQ∥BD,
∴![]() ,
,
∴EC=![]() (8-5t),ED=DC-EC=6-
(8-5t),ED=DC-EC=6-![]() (8-5t)=
(8-5t)=![]() t,
t,
∵DO=3t,
∴DE-DO=![]() t-3t=
t-3t=![]() t>0,
t>0,
∴點O在直線QM左側.
②解:如圖3中,由①可知⊙O只有在左側與直線QM相切于點H,QM與CD交于點E.
∵EC=![]() (8-5t),DO=3t,
(8-5t),DO=3t,
∴OE=6-3t-![]() (8-5t)=
(8-5t)=![]() t,
t,
∵OH⊥MQ,
∴∠OHE=90°,
∵∠HEO=∠CEQ,
∴∠HOE=∠CQE=∠CBD,
∵∠OHE=∠C=90°,
∴△OHE∽△BCD,
∴![]() ,
,
∴![]() ,
,
∴t=![]() .
.
∴t=![]() s時,⊙O與直線QM相切.
s時,⊙O與直線QM相切.
連接PM,假設PM與⊙O相切,則∠OMH=![]() PMQ=22.5°,
PMQ=22.5°,
在MH上取一點F,使得MF=FO,則∠FMO=∠FOM=22.5°,
∴∠OFH=∠FOH=45°,
∴OH=FH=![]() ,FO=FM=
,FO=FM=![]() ,
,
∴MH=![]() (
(![]() +1),
+1),
由![]() 得到HE=
得到HE=![]() ,
,
由![]() 得到EQ=
得到EQ=![]() ,
,
∴MH=MQ-HE-EQ=4-![]() -
-![]() =
=![]() ,
,
∴![]() (
(![]() +1)≠
+1)≠![]() ,矛盾,
,矛盾,
∴假設不成立.
∴直線PM與⊙O不相切.


科目:初中數學 來源: 題型:
【題目】如圖1,Rt△ABC中,∠ACB=90。 , 直角邊AC在射線OP上,直角頂點C與射線端點0重合,AC=b,BC=a,且滿足 ![]() .
.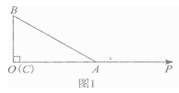
(1)求a,b的值;
(2)如圖2,向右勻速移動Rt△ABC,在移動的過程中Rt△ABC的直角邊AC在射線OP上勻速向右運動,移動的速度為1個單位/秒,移動的時間為t秒,連接OB,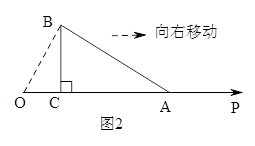
①若△OAB為等腰三角形,求t的值;
②Rt△ABC在移動的過程中,能否使△OAB為直角三角形?若能,求出t的值:若不能,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明和小紅兩人做游戲,小明對小紅說:“你任意想一個數,把這個數加上5,然后乘以2接著減去4,最后除以2,把得到的結果告訴我,我就知道你想的是什么數結果小紅把按規則計算出結果為20告訴了小明.”如果你是小明,你應該告訴小紅,她想的數是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
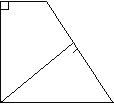
【題目】如圖,在直角梯形ABCD中,AB∥CD,AD⊥DC,AB=BC,且AE⊥BC.
(1)求證:AD=AE;
(2)若AD=8,DC=4,求AB的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com