小明和小亮玩紙牌游戲,他們從同一副撲克牌中抽出四張,牌面數字分別為3、6、10、13.游戲規則如下:將四張牌正面朝下洗勻后放在桌上,小明先從中隨機抽出一張并記下牌面上的數字,小亮再從剩余的3張中隨機抽出一張也記下牌面上的數字.若抽出的兩張牌的牌面數字都是兩位數,則小明得1分;否則,小亮得1分,若干局后得分高的人獲勝.請你判斷這個游戲規則是否公平,說明理由.
解:每次摸牌游戲所有可能出現的結果如下
| 3 | 6 | 10 | 13 |
| 3 | | (3,6) | (3,10) | (3,13) |
| 6 | (6,3) | | (6,10) | (6,13) |
| 10 | (10,3) | (10,6) | | (10,13) |
| 13 | (13,3) | (13,6) | (13,10) | |
共有12種結果,每種結果出現的可能性相同,
摸出的兩張牌的數字都為兩位數的結果有(10,13)(13,10)2種情況,
所以摸出的兩張牌的數字都為兩位數的概率是
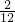
=

,小明平均每次游戲得分為1×

=

分,
其余結果出現的概率為1-

=

,即小亮平均每次游戲得分為1×

=

分,

分≠

分,所以該游戲規則不公平.
分析:先通過列表,求出抽出的兩張牌的牌面數字都是兩位數的概率,再求出其它情況的概率,然后根據若抽出的兩張牌的牌面數字都是兩位數,則小明得1分;否則,小亮得1分分別求出小明、小亮的得分即可判斷出這個游戲規則是否公平.
點評:此題考查了游戲公平性;關鍵是通過列表求出抽出的兩張牌的牌面數字都是兩位數的概率,得出兩人的最后的得分,判斷游戲公平性就要計算每個事件的概率,概率相等就公平,否則就不公平.

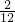 =
= ,小明平均每次游戲得分為1×
,小明平均每次游戲得分為1× =
= 分,
分, =
= ,即小亮平均每次游戲得分為1×
,即小亮平均每次游戲得分為1× =
= 分,
分, 分≠
分≠ 分,所以該游戲規則不公平.
分,所以該游戲規則不公平.
