日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

已知實數(shù)、滿足，求代數(shù)式的值。

解：∵，≥0，≥0

∴=0，=0

∴，

∴，

∴

∴

         ==2008

練習(xí)冊系列答案
相關(guān)習(xí)題

科目：初中數(shù)學(xué) 來源： 題型：閱讀理解

閱讀下列范例，按要求解答問題．
例：已知實數(shù)a，b，c滿足：a+b+2c=1，a2+b2+6c+
3
2
=0，求a，b，c的值．
解：∵a+b+2c=1，∴a+b=1-2c，
設(shè)a=
1-2c
2
+t，b=
1-2c
2
-t①
∵a2+b2+6c+
3
2
=0②
將①代入②得：(
1-2c
2
+t)2+(
1-2c
2
-t)2+6c+
3
2
=0
整理得：t2+（c2+2c+1）=0，即t2+（c+1）2=0，∴t=0，c=-1
將t，c的值同時代入①得：a=
3
2
，b=
3
2
．∴a=b=
3
2
，c=-1．
以上解法是采用“均值換元”解決問題．一般地，若實數(shù)x，y滿足x+y=m，則可設(shè)x=
m
2
+t，y=
m
2
-t，合理運用這種換元技巧，可順利解決一些問題．現(xiàn)請你根據(jù)上述方法試解決下面問題：
已知實數(shù)a，b，c滿足：a+b+c=6，a2+b2+c2=12，求a，b，c的值．

查看答案和解析>>

科目：初中數(shù)學(xué) 來源： 題型：閱讀理解

閱讀下列范例，按要求解答問題．
例：已知實數(shù)a、b、c滿足a+b+2c=1，a2+b2+6c+
3
2
=0，求a、b、c的值．
解法1：由已知得a+b=1-2c，①（a+b）2-2ab+6c+
3
2
=0．②
將①代入②，整理得4c2+2c-2ab+
5
2
=0．∴ab=2c2+c+
5
4
③
由①、③可知，a、b是關(guān)于t的方程t2-（1-2c）t+2c2+c+
5
4
=0④的兩個實數(shù)根．
∴△=（1-2c）2-4（2c2+c+
5
4
≥0，即（c+1）2≤0．而（c+1）2≥0，∴c+l=0，c=-1，
將c=-1代入④，得t2-3t+
9
4
=0．∴t1=t2=
3
2
，即a=b=
3
2
．∴a=b，c=-1．
解法2∵a+b+2c=1，∴a+b=1-2c、設(shè)a=
1-2c
2
+t，b=
1-2c
2
-t．①
∵a2+b2+6c+
3
2
=0，∴（a+b）2-2ab+6c+
3
2
=0．②
將①代入②，得（1-2c）2-2(
1-2c
2
+t)(
1-2c
2
-t)+6c+
3
2
=0．
整理，得t2+（c2+2c+1）=0，即t2+（c+1）2=0．∴t=0，c=-1．
將t、c的值同時代入①，得a=
3
2
，b=
3
2
．a(chǎn)=b=
3
2
，c=-1．
以上解法1是構(gòu)造一元二次方程解決問題．若兩實數(shù)x、y滿足x+y=m，xy=n，則x、y是關(guān)于t的一元二次方程t2-mt+n=0的兩個實數(shù)根，然后利用判別式求解．
以上解法2是采用均值換元解決問題．若實數(shù)x、y滿足x+y=m，則可設(shè)x=
m
2
+t，y=
m
2
-t．一些問題根據(jù)條件，若合理運用這種換元技巧，則能使問題順利解決．
下面給出兩個問題，解答其中任意一題：
（1）用另一種方法解答范例中的問題．
（2）選用范例中的一種方法解答下列問題：
已知實數(shù)a、b、c滿足a+b+c=6，a2+b2+c2=12，求證：a=b=c．

查看答案和解析>>

科目：初中數(shù)學(xué) 來源：藁城市一模 題型：解答題

閱讀下列范例，按要求解答問題．
例：已知實數(shù)a，b，c滿足：a+b+2c=1，a2+b2+6c+
3
2
=0，求a，b，c的值．
∵a+b+2c=1，∴a+b=1-2c，
設(shè)a=
1-2c
2
+t，b=
1-2c
2
-t①
∵a2+b2+6c+
3
2
=0②
將①代入②得：(
1-2c
2
+t)2+(
1-2c
2
-t)2+6c+
3
2
=0
整理得：t2+（c2+2c+1）=0，即t2+（c+1）2=0，∴t=0，c=-1
將t，c的值同時代入①得：a=
3
2
，b=
3
2
．∴a=b=
3
2
，c=-1．
以上解法是采用“均值換元”解決問題．一般地，若實數(shù)x，y滿足x+y=m，則可設(shè)x=
m
2
+t，y=
m
2
-t，合理運用這種換元技巧，可順利解決一些問題．現(xiàn)請你根據(jù)上述方法試解決下面問題：
已知實數(shù)a，b，c滿足：a+b+c=6，a2+b2+c2=12，求a，b，c的值．

查看答案和解析>>

科目：初中數(shù)學(xué) 來源：2010年河北省石家莊市藁城市中考數(shù)學(xué)一模試卷（解析版） 題型：解答題

閱讀下列范例，按要求解答問題．
例：已知實數(shù)a，b，c滿足：，求a，b，c的值．
解：∵a+b+2c=1，∴a+b=1-2c，
設(shè)①
∵②
將①代入②得：
整理得：t2+（c2+2c+1）=0，即t2+（c+1）2=0，∴t=0，c=-1
將t，c的值同時代入①得：．∴．
以上解法是采用“均值換元”解決問題．一般地，若實數(shù)x，y滿足x+y=m，則可設(shè)，合理運用這種換元技巧，可順利解決一些問題．現(xiàn)請你根據(jù)上述方法試解決下面問題：
已知實數(shù)a，b，c滿足：a+b+c=6，a2+b2+c2=12，求a，b，c的值．

查看答案和解析>>

科目：初中數(shù)學(xué) 來源：2002年湖北省荊門市中考數(shù)學(xué)試卷（解析版） 題型：解答題

（2002•荊門）閱讀下列范例，按要求解答問題．
例：已知實數(shù)a、b、c滿足a+b+2c=1，a2+b2+6c+=0，求a、b、c的值．
解法1：由已知得a+b=1-2c，①（a+b）2-2ab+6c+=0．②
將①代入②，整理得4c2+2c-2ab+=0．∴ab=2c2+c+③
由①、③可知，a、b是關(guān)于t的方程t2-（1-2c）t+2c2+c+=0④的兩個實數(shù)根．
∴△=（1-2c）2-4（2c2+c+≥0，即（c+1）2≤0．而（c+1）2≥0，∴c+l=0，c=-1，
將c=-1代入④，得t2-3t+=0．∴t1=t2=，即a=b=．∴a=b，c=-1．
解法2∵a+b+2c=1，∴a+b=1-2c、設(shè)a=+t，b=-t．①
∵a2+b2+6c+=0，∴（a+b）2-2ab+6c+=0．②
將①代入②，得（1-2c）2-2+6c+=0．
整理，得t2+（c2+2c+1）=0，即t2+（c+1）2=0．∴t=0，c=-1．
將t、c的值同時代入①，得a=，b=．a(chǎn)=b=，c=-1．
以上解法1是構(gòu)造一元二次方程解決問題．若兩實數(shù)x、y滿足x+y=m，xy=n，則x、y是關(guān)于t的一元二次方程t2-mt+n=0的兩個實數(shù)根，然后利用判別式求解．
以上解法2是采用均值換元解決問題．若實數(shù)x、y滿足x+y=m，則可設(shè)x=+t，y=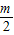-t．一些問題根據(jù)條件，若合理運用這種換元技巧，則能使問題順利解決．
下面給出兩個問題，解答其中任意一題：
（1）用另一種方法解答范例中的問題．
（2）選用范例中的一種方法解答下列問題：
已知實數(shù)a、b、c滿足a+b+c=6，a2+b2+c2=12，求證：a=b=c．

查看答案和解析>>

同步練習(xí)冊答案
主站蜘蛛池模板： jizz在亚洲 | 欧美精品国产精品 | 天天操狠狠操 | 中文字幕在线三区 | 后进极品白嫩翘臀在线视频 | 久久精品美女视频 | 国产精品久久久久久久午夜片 | 黄色毛片观看 | 国产精品国产三级国产专业不 | 黄色片视频网站 | 九九国产 | 精品自拍视频 | 欧美午夜视频在线观看 | 久久视频一区二区 | 国产免费av在线 | 精品国产区| 精品亚洲一区二区三区在线观看 | 久久99精品久久久久久久青青日本 | 欧美日韩高清 | 久久高清精品 | 国产精品一区二区三区在线 | 日本五月婷婷 | 国产一区二区三区在线 | 中文字幕乱码一区二区三区 | 美女视频黄色免费 | 韩国精品主播一区二区在线观看 | 国产视频黄在线观看 | 精品国产一区二区三区在线观看 | 国产精品视频免费看 | 激情网站免费观看 | 日韩久久久久久 | 精品一区二区三区在线视频 | 国产欧美精品一区二区三区四区 | 国产91九色一区二区三区 | 噜噜噜天天躁狠狠躁夜夜精品 | 欧美在线 | 久草免费在线 | 精品一区二区三区在线视频 | 国产 欧美 日韩 一区 | 亚洲成人一区二区三区 | 国产成人精品一区二区三区四区 |