閱讀下列范例,按要求解答問題.
例:已知實數a、b、c滿足a+b+2c=1,a
2+b
2+6c+
=0,求a、b、c的值.
解法1:由已知得a+b=1-2c,①(a+b)
2-2ab+6c+
=0.②
將①代入②,整理得4c
2+2c-2ab+
=0.∴ab=2c
2+c+
③
由①、③可知,a、b是關于t的方程t
2-(1-2c)t+2c
2+c+
=0④的兩個實數根.
∴△=(1-2c)
2-4(2c
2+c+
≥0,即(c+1)
2≤0.而(c+1)
2≥0,∴c+l=0,c=-1,
將c=-1代入④,得t
2-3t+
=0.∴t
1=t
2=
,即a=b=
.∴a=b,c=-1.
解法2∵a+b+2c=1,∴a+b=1-2c、設a=
+t,b=
-t.①
∵a
2+b
2+6c+
=0,∴(a+b)
2-2ab+6c+
=0.②
將①代入②,得(1-2c)
2-2
(+t)(-t)+6c+
=0.
整理,得t
2+(c
2+2c+1)=0,即t
2+(c+1)
2=0.∴t=0,c=-1.
將t、c的值同時代入①,得a=
,b=
.a=b=
,c=-1.
以上解法1是構造一元二次方程解決問題.若兩實數x、y滿足x+y=m,xy=n,則x、y是關于t的一元二次方程t
2-mt+n=0的兩個實數根,然后利用判別式求解.
以上解法2是采用均值換元解決問題.若實數x、y滿足x+y=m,則可設x=
+t,y=
-t.一些問題根據條件,若合理運用這種換元技巧,則能使問題順利解決.
下面給出兩個問題,解答其中任意一題:
(1)用另一種方法解答范例中的問題.
(2)選用范例中的一種方法解答下列問題:
已知實數a、b、c滿足a+b+c=6,a
2+b
2+c
2=12,求證:a=b=c.



 ,求a,b,c的值.
,求a,b,c的值. ①
① ②
②
 .∴
.∴ .
. ,合理運用這種換元技巧,可順利解決一些問題.現請你根據上述方法試解決下面問題:
,合理運用這種換元技巧,可順利解決一些問題.現請你根據上述方法試解決下面問題: =0,求a、b、c的值.
=0,求a、b、c的值. =0.②
=0.② =0.∴ab=2c2+c+
=0.∴ab=2c2+c+ ③
③ =0④的兩個實數根.
=0④的兩個實數根. ≥0,即(c+1)2≤0.而(c+1)2≥0,∴c+l=0,c=-1,
≥0,即(c+1)2≤0.而(c+1)2≥0,∴c+l=0,c=-1, =0.∴t1=t2=
=0.∴t1=t2= ,即a=b=
,即a=b= .∴a=b,c=-1.
.∴a=b,c=-1. +t,b=
+t,b= -t.①
-t.① =0,∴(a+b)2-2ab+6c+
=0,∴(a+b)2-2ab+6c+ =0.②
=0.② +6c+
+6c+ =0.
=0. ,b=
,b= .a=b=
.a=b= ,c=-1.
,c=-1. +t,y=
+t,y=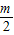 -t.一些問題根據條件,若合理運用這種換元技巧,則能使問題順利解決.
-t.一些問題根據條件,若合理運用這種換元技巧,則能使問題順利解決.