
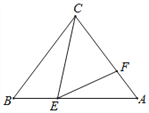
【題目】如圖,在△ABC中,已知AC=BC=5,AB=6,點E是線段AB上的動點(不與端點重合),點F是線段AC上的動點,連接CE、EF,若在點E、點F的運動過程中,始終保證∠CEF=∠B.當以點C為圓心,以CF為半徑的圓與AB相切時,則BE的長為_________.
【答案】1或5
【解析】如圖,設⊙C與BA切于點M,則CM=CF,CM⊥BA,根據等腰三角形的三線合一的性質可得BM=AM=![]() =3,在Rt△AMC中,根據勾股定理求得CM=CF= 4,從而得AF=1,再證明△AEF∽△BCE,根據相似三角形的性質可得
=3,在Rt△AMC中,根據勾股定理求得CM=CF= 4,從而得AF=1,再證明△AEF∽△BCE,根據相似三角形的性質可得![]() ,設BE長為x,則EA長為6-x,可得
,設BE長為x,則EA長為6-x,可得![]() ,解方程求得x的值,即可得BE的長.
,解方程求得x的值,即可得BE的長.
如圖,設⊙C與BA切于點M,則CM=CF,CM⊥BA,

∵CA=CB,CM⊥BA,AB=6,
∴BM=AM=![]() =3,
=3,
Rt△AMC中,AC=5,AM=3,
∴CM=CF= 4,
∴AF=1,
∵CA=CB,
∴∠B=∠A,
∵∠B+∠BCE=∠CEA=∠CEF+∠FEA,
∵∠CEF=∠B,
∴∠AEF=∠BCE;
∴△AEF∽△BCE,
∴![]() ,
,
設BE長為x,則EA長為6-x
∴![]() ,
,
解得:x1=1,x2=5,
∴BE的長為1或5.
故答案為:1或5.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
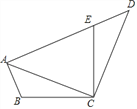
【題目】如圖,已知在四邊形ABCD中,點E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求證:AC=CD;
(2)若∠ACB=30°,∠D=45°,求∠AEC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明家需要用鋼管做防盜窗,按設計要求,其中需要長為 0.8m,2.5m 且粗細相同的鋼管分別為 100 根,32 根,并要求這些用料不能是焊接而成的.現鋼材市場的這種規格的鋼管每根為 6m.
(1)試問一根 6m 長的圓鋼管有哪些裁剪方法呢?請填寫下空(余料作廢).
方法①:當只裁剪長為 0.8m 的用料時,最多可剪 根;
方法②:當先剪下 1 根 2.5m 的用料時,余下部分最多能剪 0.8m 長的用料 根;
方法③:當先剪下 2 根 2.5m 的用料時,余下部分最多能剪 0.8m 長的用料 根.
(2)分別用(1)中的方法②和方法③各裁剪多少根 6m 長的鋼管,才能剛好得到所需要的相應數量的材料?
(3)試探究:除(2)中方案外,在(1)中還有哪兩種方法聯合,所需要 6m 長的鋼管與(2) 中根數相同?
查看答案和解析>>
科目:初中數學 來源: 題型:
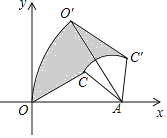
【題目】如圖,△OAC的頂點O在坐標原點,OA邊在x軸上,OA=2,AC=1,把△OAC繞點A按順時針方向旋轉到△O′AC′,使得點O′的坐標是(1,![]() ),則在旋轉過程中線段OC掃過部分(陰影部分)的面積為______.
),則在旋轉過程中線段OC掃過部分(陰影部分)的面積為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
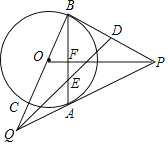
【題目】如圖,P是⊙O外的一點,PA、PB是⊙O的兩條切線,A、B是切點,PO交AB于點F,延長BO交⊙O于點C,交PA的延長交于點Q,連結AC.
(1)求證:AC∥PO;
(2)設D為PB的中點,QD交AB于點E,若⊙O的半徑為3,CQ=2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】垃圾的分類處理與回收利用,可以減少污染,節省資源.某城市環保部門為了提高宣傳實效,抽樣調查了部分居民小區一段時間內生活垃圾的分類情況,其相關信息如下:
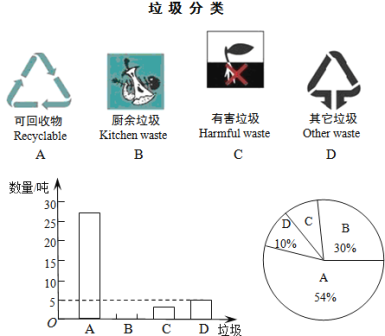
根據圖表解答下列問題:
(1)請將條形統計圖補充完整;
(2)在扇形統計圖樣中,產生的有害垃圾C所對應的圓心角 度;
(3)調查發現,在可回收物中塑料類垃圾占13%,每回收1噸塑料類垃圾可獲得0.5噸二級原料.假設該城市每月產生的生活垃圾為1000噸,且全部分類處理,那么每月回收的塑料類垃圾可以獲得多少噸二級原料?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,過點A(2,0)的直線![]() 與y軸交于點B,與雙曲線
與y軸交于點B,與雙曲線![]() 交于點P,點P位于y軸左側,且到y軸的距離為1,已知tan∠OAB=
交于點P,點P位于y軸左側,且到y軸的距離為1,已知tan∠OAB=![]() .
.
(1)分別求出直線與雙曲線相應的函數表達式;
(2)觀察圖象,直接寫出不等式![]() >
>![]() 的解集.
的解集.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在平面直角坐標系中,點![]() 在
在![]() 軸上,點
軸上,點![]() 、
、![]() 在
在![]() 軸上,
軸上,![]() ,
,![]() ,
,![]() ,點
,點![]() 的坐標是
的坐標是![]() ,
,
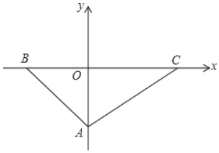
(1)求![]() 三個頂點
三個頂點![]() 、
、![]() 、
、![]() 的坐標;
的坐標;
(2)連接![]() 、
、![]() ,并用含字母
,并用含字母![]() 的式子表示
的式子表示![]() 的面積(
的面積(![]() );
);
(3)在(2)問的條件下,是否存在點![]() ,使
,使![]() 的面積等于
的面積等于![]() 的面積?如果存在,請求出點
的面積?如果存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程(組)或不等式(組)解應用題:
(1)甲工人接到240個零件的任務,工作1小時后,因要提前完成任務,調來乙和甲合作,合做了5小時完成.已知甲每小時比乙少做4個,那么甲、乙每小時各做多少個?
(2)某工廠準備購進![]() 、
、![]() 兩種機器共20臺用于生產零件,經調查2臺
兩種機器共20臺用于生產零件,經調查2臺![]() 型機器和1臺
型機器和1臺![]() 型機器價格為18萬元,1臺
型機器價格為18萬元,1臺![]() 型機器和2臺
型機器和2臺![]() 型機器價格為21萬元.
型機器價格為21萬元.
①求一臺![]() 型機器和一臺
型機器和一臺![]() 型機器價格分別是多少萬元?
型機器價格分別是多少萬元?
②已知1臺![]() 型機器每月可加工零件400個,1臺
型機器每月可加工零件400個,1臺![]() 型機器每月可加工零件800個,經預算購買兩種機器的價格不超過140萬元,每月兩種機器加工零件總數不低于12400個,那么有哪幾種購買方案,哪種方案最省錢?
型機器每月可加工零件800個,經預算購買兩種機器的價格不超過140萬元,每月兩種機器加工零件總數不低于12400個,那么有哪幾種購買方案,哪種方案最省錢?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com