
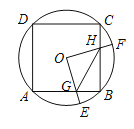
【題目】如圖,邊長為4的正方形ABCD內接于⊙O,點E是![]() 上的一動點(不與點A、B重合),點F是
上的一動點(不與點A、B重合),點F是![]() 上的一點,連接OE,OF,分別與交AB,BC于點G,H,且∠EOF=90°,連接GH,有下列結論:
上的一點,連接OE,OF,分別與交AB,BC于點G,H,且∠EOF=90°,連接GH,有下列結論:
①![]() ;②△OGH是等腰直角三角形;③四邊形OGBH的面積隨著點E位置的變化而變化;④△GBH周長的最小值為
;②△OGH是等腰直角三角形;③四邊形OGBH的面積隨著點E位置的變化而變化;④△GBH周長的最小值為![]() .其中正確的是____________.(把你認為正確結論的序號都填上)
.其中正確的是____________.(把你認為正確結論的序號都填上)
【答案】①②④
【解析】
試題①如圖1中,連接OB、OA.
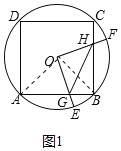
∵四邊形ABCD是正方形,
∴∠EOF=∠AOB=90°,
∴∠AOE+∠BOE=∠BOF+∠BOE,
∴∠AOE=∠BOF,
∴![]() .
.
所以①正確;
②如圖1中,在△AOG和△BOH中,
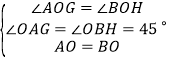 ,
,
∴△AOG≌△BOH;
∴OG=OH,
∵∠GOH=90°,
∴△OGH是等腰直角三角形.
所以②正確;
③如圖1中,
∵△AOG≌△BOH,
∴四邊形OGBH的面積=△AOB的面積=![]() 正方形ABCD的面積,
正方形ABCD的面積,
∴四邊形OGBH的面積不發生變化.
所以③錯誤;
④∵△AOG≌△BOH,
∴AG=BH,
∴BG+BH=BG+AG=BC=4,
設BG=x,則BH=4-x,
則GH=![]() =
=![]() =
=![]() ,
,
∴當x=2時GH最小,最小值為![]() ,
,
∴△GBH周長的最小值為4+![]() .
.
所以④正確.
故答案為:①②④.


 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:初中數學 來源: 題型:
【題目】解方程:
我們已經學習了一元二次方程的多種解法:如因式分解法,開平方法,配方法和公式法,還可以運用十字相乘法,請從以下一元二次方程中任選兩個,并選擇你認為適當的方法解這個方程.
①![]() ②
②![]() ③
③![]() ④
④![]()
我選擇第 個方程。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖某農場要建一個長方形的養雞場,雞場的一邊靠墻(墻長18m),另三邊用木欄圍成,木欄長35m.雞場的面積能達到150m2嗎?如果能,請你給出設計方案;如果不能,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,C是AB延長線上一點,CD與⊙O相切于點E,AD⊥CD于點D.

(1)求證:AE平分∠DAC;
(2)若AB=4,∠ABE=60°.
①求AD的長;
②求出圖中陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 是等邊
是等邊![]() 內一點,
內一點,![]() .將
.將![]() 繞點
繞點![]() 按順時針方向旋轉
按順時針方向旋轉![]() 得
得![]() ,連接
,連接![]() .
.

(1)求證:![]() 是等邊三角形;
是等邊三角形;
(2)當![]() 時,試判斷
時,試判斷![]() 的形狀,并說明理由;
的形狀,并說明理由;
(3)探究:當![]() 為多少度時,
為多少度時,![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某企業接到一批產品的生產任務,按要求必須在14天內完成.已知每件產品的出廠價為60元.工人甲第x天生產的產品數量為y件,y與x滿足如下關系:
![]()
(1)工人甲第幾天生產的產品數量為70件?
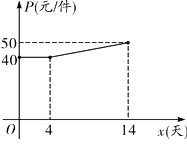
(2)設第x天生產的產品成本為P元/件,P與![]() 的函數圖象如圖.工人甲第x天創造的利潤為W元,求W與x的函數關系式,并求出第幾天時利潤最大,最大利潤是多少?
的函數圖象如圖.工人甲第x天創造的利潤為W元,求W與x的函數關系式,并求出第幾天時利潤最大,最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形OABC的頂點A,C在x,y軸正半軸上,反比例函數![]() 過OB的中點D,與BC,AB交于M,N,且已知D(m,2),N(8,n).
過OB的中點D,與BC,AB交于M,N,且已知D(m,2),N(8,n).
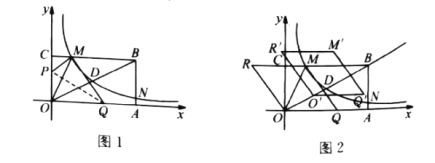
(1)求反比例函數的解析式;
(2)若將矩形一角折疊,使點O與點M重合,折痕為PQ,求點P的坐標;
(3)如圖2,若將![]() 沿OM向左翻折,得到菱形OQMR,將該菱形沿射線OB以每秒
沿OM向左翻折,得到菱形OQMR,將該菱形沿射線OB以每秒![]() 個單位向上平移t秒.
個單位向上平移t秒.
① 用t的代數式表示![]() 和
和![]() 的坐標;
的坐標;
② 要使該菱形始終與反比例函數圖像有交點,求t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知二次函數![]() (a、b、c為常數,a≠0)的圖象過點O(0,0)和點A(4,0),函數圖象最低點M的縱坐標為
(a、b、c為常數,a≠0)的圖象過點O(0,0)和點A(4,0),函數圖象最低點M的縱坐標為![]() ,直線l的解析式為y=x.
,直線l的解析式為y=x.
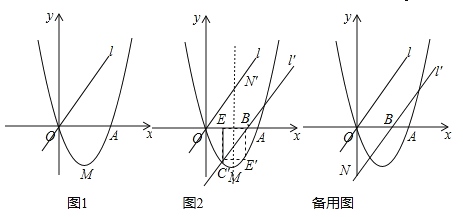
(1)求二次函數的解析式;
(2)直線l沿x軸向右平移,得直線l′,l′與線段OA相交于點B,與x軸下方的拋物線相交于點C,過點C作CE⊥x軸于點E,把△BCE沿直線l′折疊,當點E恰好落在拋物線上點E′時(圖2),求直線l′的解析式;
(3)在(2)的條件下,l′與y軸交于點N,把△BON繞點O逆時針旋轉135°得到△B′ON′,P為l′上的動點,當△PB′N′為等腰三角形時,求符合條件的點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com