Question

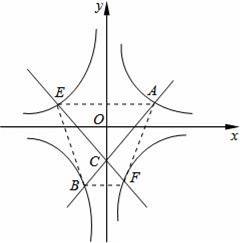
如圖，在平面直角坐標系中，雙曲線y=與一次函數y=kx+b（k＞0）分別交于點A與點B，直線與y軸交于點C，把直線AB繞著點C旋轉一定的角度后，得到一條新直線．若新直線與雙曲線y=﹣相交于點E、F，并使得雙曲線y=，y=﹣，連線y=kx+b以及新直線構成的圖形能關于某條坐標軸對稱，如果點A的橫坐標為1，則當k為多少時，點A、點E、點B、點F構成的四邊形的面積最小．最小值是多少？

Answer 1

【考點】反比例函數綜合題．

【分析】將A橫坐標代入反比例y=中，求出y的值確定出A的縱坐標，將A坐標代入y=kx+b中表示出b，得到一次函數解析式，與反比例解析式聯立，消去y得到關于x的一元二次方程，求出方程的解表示出B坐標，由雙曲線y=與y=﹣與直線y=kx+b以及新直線的對稱性可得：點A與點E關于y軸對稱，點B與點F關于y軸對稱，表示出E與F坐標，進而確定出AE與BF，且AE與BF的距離為k+1，利用梯形的面積公式表示出梯形AEBF的面積即可．

【解答】解：∵x_A=1，A點在y=上，

∴y_A=1，

把點A（1，1）代入y=kx+b中得：1=k+b，

∴b=1﹣k，

∴y=kx+（1﹣k），

由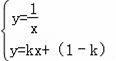，消去y得： =kx+（1﹣k），

整理得：kx²+（1﹣k）x﹣1=0，

∴x₁=1，x₂=﹣，

∴點B的坐標為（﹣，﹣k），

由雙曲線y=與y=﹣與直線y=kx+b以及新直線的對稱性可得：

點A與點E關于y軸對稱，點B與點F關于y軸對稱，

∴E（﹣1，1）、F（，﹣k），

∴AE=2，BF=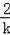，AE與BF的距離為k+1，

∴S_梯形AEBF=（k+1）=（1+）（k+1）=k++2，

∵k＞0∴當k=1時，梯形S_AEBF有最小值4．

【點評】此題屬于反比例函數綜合題，涉及的知識有：待定系數法確定函數解析式，一次函數與反比例函數的交點，坐標與圖形性質，以及對稱的性質，由雙曲線y=與y=﹣與直線y=kx+b以及新直線的對稱性可得：點A與點E關于y軸對稱，點B與點F關于y軸對稱是解本題的關鍵．