
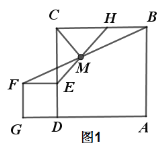
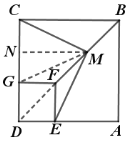
【題目】如圖1,點E是正方形ABCD邊CD上任意點,以DE為邊作正方形DEFG,連接BF.點M是線段BF中點,射線EM與BC交于點H,連接CM.
(1)請直接寫出CM和EM的數量關系和位置關系:__________;
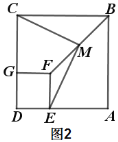
(2)把圖1中的正方形DEFG繞點D順時針旋轉90°,此時點E、G恰好分別落在線段AD、CD上,如圖2所示,其他條件不變,(1)中的結論是否成立,請說明理由.
(3)若DG=![]() ,AB=4.
,AB=4.
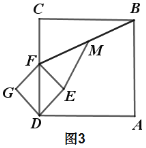
①把圖1中的正方形DEFG繞點D順時針旋轉45°,此時點F恰好落在線段CD上,連接EM,如圖3所示,其他條件不變,計算EM的長度;
②若把圖1中的正方形DEFG繞點D順時針旋轉一周,請直接寫出EM的最大值.
【答案】(1)![]() .(2)成立,具體利用見解析;(3)①
.(2)成立,具體利用見解析;(3)①![]() ;②
;②![]() .
.
【解析】
(1)證明![]() ,得到HM=EM,根據等腰之間三角形的性質即可得到;
,得到HM=EM,根據等腰之間三角形的性質即可得到;
(2)連接DF,MG,作![]() 于N,可證得
于N,可證得![]() ,得到ME=MG,
,得到ME=MG,![]() ,再由M為BF的中點,
,再由M為BF的中點,![]() ,得到GN=NC,進一步可得到,又
,得到GN=NC,進一步可得到,又![]() ,
,![]() ,再由角度的關系可得到
,再由角度的關系可得到![]() ,即可得到結論.
,即可得到結論.
(3)①連接BE,CE,過點E作![]() 于點H,根據正方形的性質可推出
于點H,根據正方形的性質可推出![]() ,
,![]() ,證明
,證明![]() ,進一步可得到△CME是等腰直角三角形,根據之間三角形的性質求解即可.
,進一步可得到△CME是等腰直角三角形,根據之間三角形的性質求解即可.
②由條件可證的△CME為等腰直角三角形,當CE最大時,EM最大,當點E旋轉至D點下方時,且C,D,E共線時CE最大,此時CE=![]() ,再根據勾股定理即可求解.
,再根據勾股定理即可求解.
(1)結論:![]() .
.
理由:如圖1中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
在△FME和△BMH中,
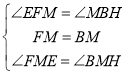 ,
,
∴![]() ,
,
∴HM=EM,EF=BH.
∵CD=BC,
∴CE=CH,
又∵![]() ,HM=EM,
,HM=EM,
∴![]() .
.
(2)![]() .
.
理由:如圖,連接DF,MG,作![]() 于N,
于N,
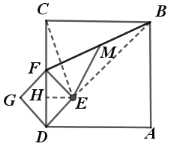
在△EDM和△GDM中,
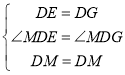 ,
,
∴![]() ,
,
∴ME=MG,![]() ,
,
∵M為BF的中點,![]() ,
,
∴GN=NC,
又![]() ,
,
∴MC=ME,
∴MC=MG,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴(1)中結論成立.
(3)①解:如圖,連接BE,CE,過點E作![]() 于點H,
于點H,
∵四邊形ABCD和四邊形EDGH是正方形,
∴![]() ,
,![]() ,
,
∴點B、E、D在同一條直線上,
∵![]() ,
,![]() ,M為BF的中點,
,M為BF的中點,
∴![]() ,
,![]() ,
,
∴CM=ME,
又∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴△CME是等腰直角三角形,![]() ,
,
在Rt△CME中,![]() ,
,![]() ,
,
∴EH=DH=1,
∴CH=4-1=3,
在Rt△CHE中,![]() ,
,
∴![]() .
.
②由上問可知![]() 一直成立,
一直成立,
∴△CME為等腰直角三角形,
∴當CE最大時,EM最大,
當點E旋轉至D點下方時,且C,D,E共線時CE最大,
此時CE=![]() .
.
設CM=EM=x,
則![]() ,
,
解得![]() ,
,
∴EM的最大值為![]() .
.


 期末100分闖關海淀考王系列答案
期末100分闖關海淀考王系列答案科目:初中數學 來源: 題型:
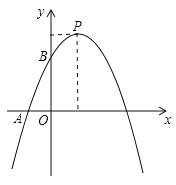
【題目】如圖,已知二次函數![]() 的圖象與x軸負半軸交于點A(-1,0),與y軸正半軸交與點B,頂點為P,且OB=3OA,一次函數y=kx+b的圖象經過A、B.
的圖象與x軸負半軸交于點A(-1,0),與y軸正半軸交與點B,頂點為P,且OB=3OA,一次函數y=kx+b的圖象經過A、B.
(1) 求一次函數解析式;
(2)求頂點P的坐標;
(3)平移直線AB使其過點P,如果點M在平移后的直線上,且![]() ,求點M坐標;
,求點M坐標;
(4)設拋物線的對稱軸交x軸與點E,聯結AP交y軸與點D,若點Q、N分別為兩線段PE、PD上的動點,聯結QD、QN,請直接寫出QD+QN的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
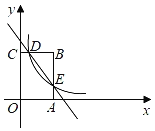
【題目】如圖,矩形OABC的頂點A,C分別在x軸和y軸上,點B的坐標為(4,6).反比例函數y=![]() (x>0)的圖象經過BC的中點D,與AB交于點E,連接DE.
(x>0)的圖象經過BC的中點D,與AB交于點E,連接DE.
(1)求k的值;
(2)求直線DE的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】襄陽臥龍大橋橫跨漢江,是我市標志性建筑之一.某校數學興趣小組在假日對豎立的索塔在橋面以上的部分(上塔柱BC和塔冠BE)進行了測量.如圖所示,最外端的拉索AB的底端A到塔柱底端C的距離為121m,拉索AB與橋面AC的夾角為37°,從點A出發沿AC方向前進23.5m,在D處測得塔冠頂端E的仰角為45°.請你求出塔冠BE的高度(結果精確到0.1m.參考數據sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41).
≈1.41).

查看答案和解析>>
科目:初中數學 來源: 題型:
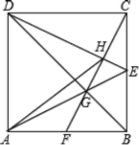
【題目】如圖,正方形ABCD的邊長為6,點E是BC的中點,連接AE與對角線BD交于點G,連接CG并延長,交AB于點F,連接DE交CF于點H,連接AH.以下結論:①CF⊥DE;②![]() ;③AD=AH;④GH=
;③AD=AH;④GH=![]() ,其中正確結論的序號是__________.
,其中正確結論的序號是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某校初二學生每周上網的時間,兩位學生進行了抽樣調查.小麗調查了初二電腦愛好者中40名學生每周上網的時間;小杰從全校400名初二學生中隨機抽取了40名學生,調查了每周上網的時間.小麗與小杰整理各自樣本數據,如下表所示:
時間段 (小時/周) | 小麗抽樣 人數 | 小杰抽樣 人數 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每組可含最低值,不含最高值)
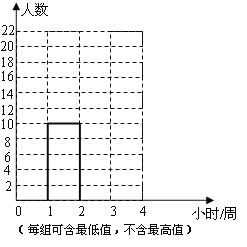
(1)你認為哪位同學抽取的樣本不合理?請說明理由;
(2)根據合理抽取的樣本,把上圖中的頻數分布直方圖補畫完整;
(3)專家建議每周上網2小時以上(含2小時)的同學應適當減少上網的時間,估計該校全體初二學生中有多少名同學應適當減少上網的時間?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據某網站調查,2019年網民最關注的熱點話題分別是:消費、教育、環保、反腐及其他共五類,根據調查的部分相關數據繪制的統計圖如圖:
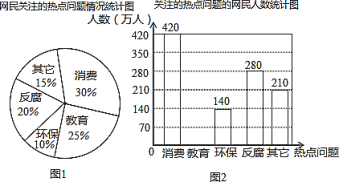
根據以上信息解答下列問題:
(1)請補全條形圖,并在圖中標明相應數據.
(2)若某市中心城區約有90萬人口,請你估計該市中心城區最關注教育問題的人數約有多少萬人?
(3)據統計,2017年網民最關注教育問題的人數所占百分比約為10%,則從2017年到2019年關注該問題網民數的年平均增長率約為多少?(已知2017~2019年每年接受調查的網民人數相同,![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com