
【題目】小民對函數![]() 的圖象和性質進行了探究.已知當自變量
的圖象和性質進行了探究.已知當自變量![]() 的值為
的值為![]() 時,函數值為
時,函數值為![]() ;當自變量的值為
;當自變量的值為![]() 時,函數值為
時,函數值為![]() .探究過程如下,請補充完整,
.探究過程如下,請補充完整,
(1)求這個函數的表達式;
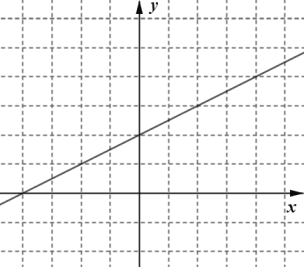
(2)在給出的平面直角坐標系中畫出這個函數的圖象并寫出這個函數的一條性質:___________;
(3)進一步探究函數圖象并解決問題:已知函數![]() 的圖象如圖所示,請結合你所畫的函數圖象,直接寫出不等式
的圖象如圖所示,請結合你所畫的函數圖象,直接寫出不等式![]() 的解集:___________.
的解集:___________.
【答案】(1)y1=|x-2|+![]() |x|;(2)當x=2時,此函數有最小值1;(3)x≥4或x≤0.
|x|;(2)當x=2時,此函數有最小值1;(3)x≥4或x≤0.
【解析】
(1)把(1,![]() ),(-1,
),(-1,![]() )代入
)代入![]() 可得關于a、b的二元一次方程組,解方程組求出a、b的值即可得答案;
可得關于a、b的二元一次方程組,解方程組求出a、b的值即可得答案;
(2)分x<0,0≤x<2,x≥2三種情況,分別利用描點法畫出圖象,根據圖象寫出相關性質即可;
(3)根據圖象找出![]() 的圖象在
的圖象在![]() 圖象上方的部分所對應的x的取值范圍即可.
圖象上方的部分所對應的x的取值范圍即可.
(1)∵當自變量![]() 的值為
的值為![]() 時,函數值為
時,函數值為![]() ;當自變量的值為
;當自變量的值為![]() 時,函數值為
時,函數值為![]() ,
,
∴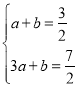 ,
,
解得:![]() ,
,
∴這個函數的表達式為y1=|x-2|+![]() |x|.
|x|.
(2)列表如下:
x | …… | -2 | -1 | 0 | 1 | 2 | 3 | 4 | …… |
y1 | …… | 5 |
| 2 |
| 1 |
| 4 | …… |
當x<0時,y1=![]() x+2,
x+2,
當0≤x<2時,y1=![]() x+2,
x+2,
當x≥2時,y1=![]() x-2,
x-2,
∴描點畫圖如下:
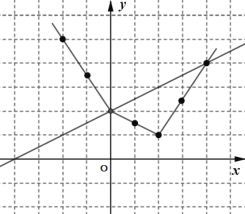
由圖象可知:當x=2時,此函數有最小值1.
(3)由圖象可知:x≥4或x≤0時,![]() 的圖象在
的圖象在![]() 圖象上方,
圖象上方,
∴不等式![]() 的解集為:x≥4或x≤0.
的解集為:x≥4或x≤0.
故答案為:x≥4或x≤0


 品學雙優卷系列答案
品學雙優卷系列答案 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案科目:初中數學 來源: 題型:
【題目】十九大召開后,某社區開展了“市民對十九大的關注情況”調查,采用隨機抽樣的方法訪問了部分年齡在18周歲以上的城鄉居民.小聰根據調查數據繪制了如下不完整的頻數分布置表和扇形統計圖.請根據圖表解答下列問題.
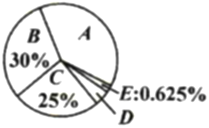
關注情況 | 頻數 |
非常關注( | 128 |
比較關注( | |
一般關注( | 80 |
不太關注( | |
不關注( | 2 |
(1)請完成頻數分布表空格數據填寫;
(2)求“非常關注”部分扇形圓心角的度數;
(3)若該社區18周歲以上居民共有20000人,請估計“比較關注”和“非常關注”的居民共有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 的正方形網格中,每個小正方形的邊長均為1,
的正方形網格中,每個小正方形的邊長均為1,![]() 的三個頂點均在小正方形的頂點上.
的三個頂點均在小正方形的頂點上.
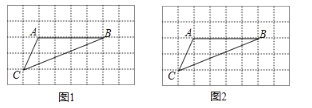
(1)在圖1中畫一個![]() (點
(點![]() 在小正方形的頂點上),使
在小正方形的頂點上),使![]() 的周長等于
的周長等于![]() 的周長,且以
的周長,且以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是軸對稱圖形;
為頂點的四邊形是軸對稱圖形;
(2)在圖2中畫![]() (點
(點![]() 在小正方形的頂點上),使
在小正方形的頂點上),使![]() 的周長等于
的周長等于![]() 的周長,且以
的周長,且以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是中心對稱圖形;
為頂點的四邊形是中心對稱圖形;
(3)直接寫出圖2中四邊形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《小豬佩奇》這部動畫片,估計同學們都非常喜歡.周末,小豬佩奇一家4口人(小豬佩奇,小豬喬治,小豬媽媽,小豬爸爸)到一家餐廳就餐,包廂有一圓桌,旁邊有四個座位(![]() ,
,![]() ,
,![]() ,
,![]() ).
).


(1)小豬佩奇隨機坐到![]() 座位的概率是________;
座位的概率是________;
(2)若現在由小豬佩奇,小豬喬治兩人先后選座位,用樹狀圖或列表的方法計算出小豬佩奇和小豬喬治坐對面的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形具有不穩定性,如圖,在平面直角坐標系![]() 中,矩形
中,矩形![]() 的邊
的邊![]() 在
在![]() 軸上,且點
軸上,且點![]() ,邊
,邊![]() 長為
長為![]() .現固定邊
.現固定邊![]() ,向右推動矩形使點
,向右推動矩形使點![]() 落在
落在![]() 軸上(落點記為
軸上(落點記為![]() ),點
),點![]() 的對應點記為
的對應點記為![]() ,已知矩形
,已知矩形![]() 與推動后形成的平行四邊形
與推動后形成的平行四邊形![]() 的面積比為
的面積比為![]() ,則點
,則點![]() 坐標為_______.
坐標為_______.
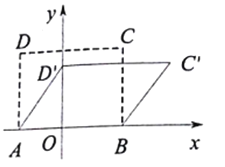
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,![]() 的直徑
的直徑![]() ,點
,點![]() 是
是![]() 延長線上的一點,過
延長線上的一點,過![]() 點作
點作![]() 的切線,切點為
的切線,切點為![]() ,連接
,連接![]() .
.

(1)若![]() ,求
,求![]() 的長;
的長;
(2)若點![]() 在
在![]() 的延長線上運動,
的延長線上運動,![]() 的平分線交
的平分線交![]() 于點
于點![]() ,你認為
,你認為![]() 的大小是否發生變化?若變化,請說明理由;若不變化,求出
的大小是否發生變化?若變化,請說明理由;若不變化,求出![]() 的大小.
的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC,∠ACB=90°,BC=3,AC=4,小紅按如下步驟作圖:
①分別以A、C為圓心,以大于![]() AC的長為半徑在AC兩邊作弧,交于兩點M、N;
AC的長為半徑在AC兩邊作弧,交于兩點M、N;
②連接MN,分別交AB、AC于點D、O;
③過C作CE∥AB交MN于點E,連接AE、CD.
則四邊形ADCE的周長為( )

A. 10 B. 20 C. 12 D. 24
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() ,
,![]() 為射線
為射線![]() 上一定點,點
上一定點,點![]() 關于射線
關于射線![]() 的對稱點為點
的對稱點為點![]() 為射線
為射線![]() 上一動點,連接
上一動點,連接![]() ,滿足
,滿足![]() 為鈍角,以點
為鈍角,以點![]() 為中心,將線段
為中心,將線段![]() 逆時針旋轉
逆時針旋轉![]() 至線段
至線段![]() ,滿足點
,滿足點![]() 在射線
在射線![]() 的反向延長線上.
的反向延長線上.
(1)依題意補全圖形;
(2)當點![]() 在運動過程中,旋轉角
在運動過程中,旋轉角![]() 是否發生變化?若不變化,請求出
是否發生變化?若不變化,請求出![]() 的值,若變化,請說明理由;
的值,若變化,請說明理由;
(3)從點![]() 向射線
向射線![]() 作垂線,與射線
作垂線,與射線![]() 的反向延長線交于點
的反向延長線交于點![]() ,探究線段
,探究線段![]() 和
和![]() 的數量關系并證明.
的數量關系并證明.
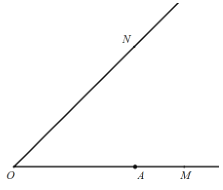
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲乙兩個工廠同時加工一批機器零件.甲工廠先加工了兩天后停止加工,維修設備,當維修完設備時,甲乙兩廠加工的零件數相等,甲工廠再以原來的工作效率繼續加工這批零件.甲乙兩廠加工零件的數量![]() (件),
(件),![]() (件)與加工件的時間
(件)與加工件的時間![]() (天)的函數圖象如圖所示,
(天)的函數圖象如圖所示,

(1)乙工廠每天加工零件的數為_____件;
(2)甲工廠維修設備的時間是多少天?
(3)求甲維修設備后加工零件的數量![]() (件)與加工零件的時間
(件)與加工零件的時間![]() (天)的函數關系式,并寫出自變量
(天)的函數關系式,并寫出自變量![]() 的取值范圍
的取值范圍
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com