解:(1)∵關于x的一元二次方程x
2+2ax+b
2=0有實數根,
∴△=(2a)
2-4b
2≥0,
有a
2-b
2≥0,
(a+b)(a-b)≥0.
∵a>0,b>0,
∴a+b>0,a-b≥0.
∴a≥b.
(2)∵a:b=2:

,
∴設
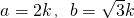
.
解關于x的一元二次方程x
2+4kx+3k
2=0,得x=-k或-3k.
當x
1=-k,x
2=-3k時,由2x
1-x
2=2得k=2.
當x
1=-3k,x
2=-k時,由2x
1-x
2=2得
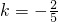
(不合題意,舍去).
∴
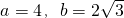
.
(3)當
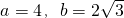
時,
二次函數y=x
2+8x+12與x軸的交點坐標分別為A(-6,0)、C(-2,0),
與y軸交點坐標為B(0,12),頂點坐標D為(-4,-4).
設z=3x-y,則y=3x-z.
畫出函數y=x
2+8x+12和y=3x的圖象,若直線y=3x平行移動時,如圖
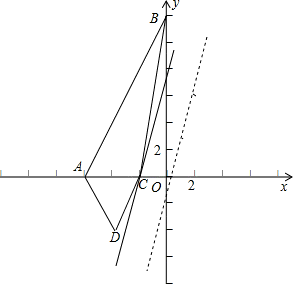
可以發現當直線經過點C時符合題意,此時最大z的值等于-6
分析:(1)根據方程有實數根可以得到其根的判別式為非負數,然后再根據a>0,b>0作出判斷即可;
(2)利用a與b的比值分別設出a和b,利用根與系數的關系用設出的未知數表示出方程的兩個解,代入的2x
1-x
2=2中求得a與b的值即可;
(3)將上題中求得的a與b的值代入到函數中確定函數的解析式,然后求得與x軸的交點坐標,與y軸的交點坐標和頂點坐標,據此可以求出3x-y的最大值.
點評:本題考查了函數綜合知識,函數綜合題是初中數學中覆蓋面最廣、綜合性最強的題型.近幾年的中考壓軸題多以函數綜合題的形式出現.解決函數綜合題的過程就是轉化思想、數形結合思想、分類討論思想、方程思想的應用過程.

 ,且2x1-x2=2,求a,b的值;
,且2x1-x2=2,求a,b的值; ,
,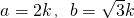 .
.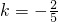 (不合題意,舍去).
(不合題意,舍去).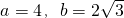 .
.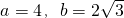 時,
時,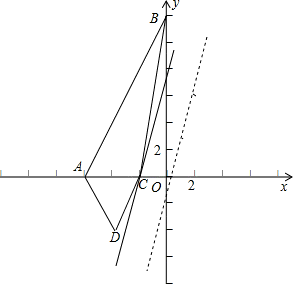


 名校課堂系列答案
名校課堂系列答案 .
. .
.