
【題目】方程 2x 2 - x + 1 = 0的根的情況是( )
A. 有一個實數根B. 有兩個不相等的實數根
C. 沒有實數根D. 有兩個相等的實數根
科目:初中數學 來源: 題型:
【題目】閱讀材料并解答問題:
關于勾股定理的研究有一個很重要的內容是勾股數組,在數學課本中我們已經了解到,“能夠成為直角三角形三條邊的三個正整數稱為勾股數”,以下是畢達哥拉斯等學派研究出的確定勾股數組的兩種方法:
方法1:若m為奇數(m≥3),則a=m,b=![]() (m2﹣1)和c=
(m2﹣1)和c=![]() (m2+1)是勾股數.
(m2+1)是勾股數.
方法2:若任取兩個正整數m和n(m>n),則a=m2﹣n2,b=2mn,c=m2+n2是勾股數.
(1)在以上兩種方法中任選一種,證明以a,b,c為邊長的△ABC是直角三角形;
(2)某園林管理處要在一塊綠地上植樹,使之構成如下圖所示的圖案景觀,該圖案由四個全等的直角三角形組成,要求每個三角形頂點處都植一棵樹,各邊上相鄰兩棵樹之間的距離均為1米,如果每個三角形最短邊上都植6棵樹,且每個三角形的各邊長之比為5:12:13,那么這四個直角三角形的邊長共需植樹 棵.
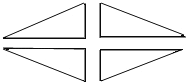
(3)某家俱市場現有大批如圖所示的梯形邊角余料(單位:cm),實驗初中數學興趣小組決定將其加工成等腰三角形,且方案如下:
三角形中至少有一邊長為10 cm;三角形中至少有一邊上的高為8 cm,
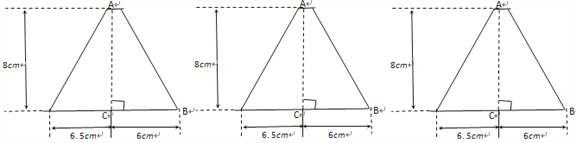
請設計出三種面積不同的方案并在圖上畫出分割線,求出相應圖形面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,CD⊥AB,EF⊥AB,垂足分別為D、F,∠1=∠2,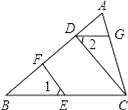
(1)試判斷DG與BC的位置關系,并說明理由.
(2)若∠A=70°,∠B=40°,求∠AGD的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用配方法解一元二次方程 x2﹣4x﹣7=0 時,需要將原方程化為( )
A. (x + 2)2 =11B. (x+2)2= 7
C. (x﹣2)2 =11D. (x﹣2)2= 7
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com