
如圖所示,P為矩形ABCD內一點,PA=3,PD=4,PC=5,求PB的長.

|
如圖所示,將△ADP平移至△BCG,使A、D分別重合于B、C,連結PG交BC于O點.
∵AP ∴PG∥AB.又AB⊥BC,∴PG⊥BC. 在Rt△OPC中,PC2=OP2+OC2, 在Rt△OBG中,BG2=OG2+OB2, ∴PC2+BG2=OG2+OB2+OP2+OC2. 同理PB2+CG2=OG2+OB2+OP2+OC2. ∴PC2+BG2=PB2+CG2. 又PC=5,BG=PA=3,CG=PD=4, ∴PB2=PC2+BG2-CG2=32+52-42=18. ∴PB= 所以PB的長是 解析:已知條件PA、PC、PD的長和問題PB的長難以直接聯系,同時又感覺到了3、4、5這一組數據非常好,不妨來考慮能否將它們放在同一個基本圖形中. 說明:利用平移變換,將條件和問題有機結合,最終解決問題. |


科目:初中數學 來源: 題型:
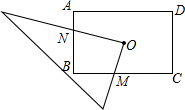 如圖所示,O為矩形ABCD的對稱中心,將直角三角板的直角頂點與O點重合,轉動三角板使兩直角邊始終與BC、AB相交,交點分別為M、N.如果AB=6,AD=8,OM=x,ON=y,則y與x的關系是
如圖所示,O為矩形ABCD的對稱中心,將直角三角板的直角頂點與O點重合,轉動三角板使兩直角邊始終與BC、AB相交,交點分別為M、N.如果AB=6,AD=8,OM=x,ON=y,則y與x的關系是| 4 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
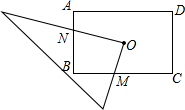
 如圖所示,O為矩形ABCD的對稱中心,將直角三角板的直角頂點與O點重合,轉動三角板使兩直角邊始終與BC、AB相交,交點分別為M、N.如果AB=6,AD=8,OM=x,ON=y,則y與x的關系是________(不填x的取值范圍)
如圖所示,O為矩形ABCD的對稱中心,將直角三角板的直角頂點與O點重合,轉動三角板使兩直角邊始終與BC、AB相交,交點分別為M、N.如果AB=6,AD=8,OM=x,ON=y,則y與x的關系是________(不填x的取值范圍)查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
查看答案和解析>>
科目:初中數學 來源:2009年黑龍江省(鶴、伊、雙、綏)升學大考數學試卷(五)(解析版) 題型:填空題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com