
 若在國外銷售,平均每件產品的利潤y2(元)與國外的銷售數量t(千件)的關系為:
若在國外銷售,平均每件產品的利潤y2(元)與國外的銷售數量t(千件)的關系為:
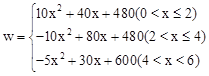 ;(3)該公司每年國內、國外的銷售量各為4千件、2千件,可使公司每年的總利潤最大,最大值為64萬元.
;(3)該公司每年國內、國外的銷售量各為4千件、2千件,可使公司每年的總利潤最大,最大值為64萬元.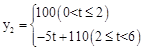 以及t=6-x即可求出y2與x的函數關系:當0<x≤4時,y2=5x+80;當y2=100時,
以及t=6-x即可求出y2與x的函數關系:當0<x≤4時,y2=5x+80;當y2=100時, ,即
,即 ,解得
,解得 ;(2)根據總利潤=國內銷售的利潤+國外銷售的利潤,結合函數解析式,分三種情況討論:①0<x≤2;②2<x≤4;③4<x<6;(3)先利用配方法將各解析式寫成頂點式,再根據二次函數的性質,求出三種情況下的最大值,再比較即可.
;(2)根據總利潤=國內銷售的利潤+國外銷售的利潤,結合函數解析式,分三種情況討論:①0<x≤2;②2<x≤4;③4<x<6;(3)先利用配方法將各解析式寫成頂點式,再根據二次函數的性質,求出三種情況下的最大值,再比較即可.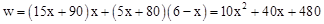 ;
; ;
; .
.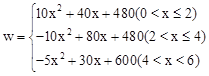 .
. ,此時x=2時,w最大=600;
,此時x=2時,w最大=600; ,此時x=4時,w最大=640;
,此時x=4時,w最大=640; ,∴4<x<6時,w<640.
,∴4<x<6時,w<640.

 培優好卷單元加期末卷系列答案
培優好卷單元加期末卷系列答案 一線名師權威作業本系列答案
一線名師權威作業本系列答案科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com