
【題目】(1)已知: ![]() ,
, ![]() 求作:
求作: ![]() ,使得
,使得![]() ,
, ![]() .
.
 作圖:
作圖:
(2)如圖,已知![]() ,求作射線OC,使OC平分
,求作射線OC,使OC平分![]() .
.
作射線OC;
在OA和OB上分別截取OD,OE,使OD=OE;
分別以點D,E為圓心,以大于![]() 長為半徑,
長為半徑,
在![]() 內作弧,兩弧交于點C.上述做法合理的順序是_____________.(寫序號)
內作弧,兩弧交于點C.上述做法合理的順序是_____________.(寫序號)

這樣做出的射線OC就是∠O 的角平分線,其依據是___________________.
【答案】(1)見解析;(2)②③①,三邊分別相等的兩個三角形全等,全等三角形的對應角相等.
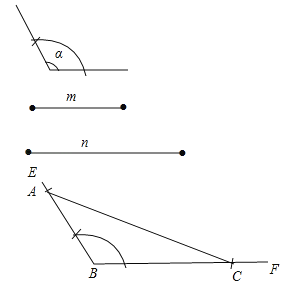
【解析】試題分析:(1)①作∠EBC=∠α,②在射線BE上截取BA=m,在射線BF上截取BC=n,連接AC.△ABC即為所求;
(2)先根據角平分線的作法進行判斷,再根據圖形進行說理,運用全等三角形的判定與性質進行證明,進而得出結論.
試題解析:(1)如圖,①作∠EBC=∠α,②在射線BE上截取BA=m,在射線BF上截取BC=n,連接AC.△ABC即為所求.
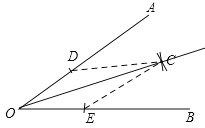
(2)解:已知∠AOB,求作射線OC,使OC平分∠AOB.
步驟為:
第一步:在OA和OB上分別截取OD,OE,使OD=OE;
第二步:分別以D,E為圓心,大于![]() DE的長為半徑作弧,在∠AOB內,兩弧交于C;
DE的長為半徑作弧,在∠AOB內,兩弧交于C;
第三步:作射線OC.
故作法合理的順序為②③①.
如圖所示,連接CD,CE,由題可得,OD=OE,CD=CE,在△OCD和△OCE中,∵OD=OE,CD=CE,OC=OC,∴△OCD≌△OCE(SSS),∴∠COD=∠COE(全等三角形的對應角相等),∴OC是∠AOB的平分線(角平分線定義).
故答案為:②③①,三邊分別相等的兩個三角形全等,全等三角形的對應角相等.


科目:初中數學 來源: 題型:
【題目】如圖①,在△ABC中,∠ACB=90°,AC=BC,過點C在△ABC外作直線MN,AM⊥MN于點M,BN⊥MN于點N.
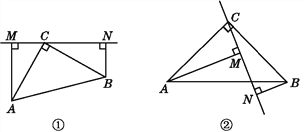
(1)試說明:MN=AM+BN.
(2)如圖②,若過點C作直線MN與線段AB相交,AM⊥MN于點M,BN⊥MN于點N(AM>BN),(1)中的結論是否仍然成立?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校學生會準備調查全校七年級學生 每天(除課間操外)的課外鍛煉時間。
(1)確定調查方式時,甲說:“我到(1)班去調查全體同學”;乙同學說:“我到體育場上去詢問參加鍛煉的同學”;丙同學說:“我到全校七年級每個班去隨機調查一定數量的同學”。你認為調查方式最合理的是(填“甲”、或“乙”或“丙”)_________
(2)他們采用了最為合適的調查方法收集數據,并繪制出如圖1所示的條形統計圖和如圖2所示的扇形統計圖,請將兩幅統計圖補充完整;


(3)若該七年級共有1200名同學,請你估計其中每天(除課間操外)課外鍛煉時間不大于20分鐘的人數。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市對當年初中升高中數學考試成績進行抽樣分析,試題滿分100分,將所得成績(均為整數)整理后,繪制了如圖所示的統計圖,根據圖中所提供的信息,回答下列問題:

(1)共抽取了多少名學生的數學成績進行分析?
(2)如果80分以上(包括80分)為優生,估計該年的優生率為多少?
(3)該年全市共有22000人參加初中升高中數學考試,請你估計及格(60分及60分以上)人數大約為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形的邊OA在x軸上,邊OC在y軸上,點B的坐標為(10,8),沿直線OD折疊矩形,使點A正好落在BC上的E處,E點坐標為(6,8),拋物線y=ax2+bx+c經過O、A、E三點.


(1)求此拋物線的解析式;
(2)求AD的長;
(3)點P是拋物線對稱軸上的一動點,當△PAD的周長最小時,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料
通過小學的學習我們知道,分數可分為“真分數”和“假分數”.而假分數都可化為帶分數,如: ![]() .
.
我們定義:在分式中,對于只含有一個字母的分式,當分子的次數大于或等于分母的次數時,我們稱之為“假分式”;當分子的次數小于分母的次數時,我們稱之為“真分式”.
如: ![]() ,
, ![]() 這樣的分式就是假分式;再如:
這樣的分式就是假分式;再如: ![]() ,
, ![]() 這樣的分式就是真分式.
這樣的分式就是真分式.
類似的,假分式也可以化為帶分式(即:整式與真分式的和的形式).
如: ![]() ;
; ![]() ;
;
再如: ![]() .
.
解決下列問題:
(1)分式![]() 是 分式(填“真分式”或“假分式”);
是 分式(填“真分式”或“假分式”);
(2)假分式![]() 可化為帶分式 的形式;
可化為帶分式 的形式;
(3)如果分式![]() 的值為整數,那么x的整數值為 .
的值為整數,那么x的整數值為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法:
①兩點之間的所有連線中,線段最短;②過一點有且只有一條直線與已知直線垂直;③連接直線外一點與直線上各點的所有線段中,垂線段最短;④直線外一點到這條直線的垂線段叫做點到直線的距離.
其中正確的個數有( )
A.4個B.3個C.2個D.1個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com