
【題目】(2011貴州安順,16,4分)如圖,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按圖中所示方法將△BCD沿BD折疊,使點C落在AB邊的C′點,那么△ADC′的面積是 .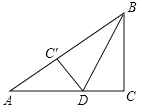
【答案】6cm2
【解析】
先根據勾股定理得到AB=10cm,再根據折疊的性質得到DC=DC′,BC=BC′=6cm,則AC′=4cm,設DC=xcm,在Rt△ADC′中根據勾股定理列方程求得x的值,然后根據三角形的面積公式計算即可.
∵∠C=90°,BC=6cm,AC=8cm,
∴AB=10cm,
∵將△BCD沿BD折疊,使點C落在AB邊的C′點,
∴△BCD≌△BC′D,
∴∠C=∠BC′D=90°,DC=DC′,BC=BC′=6cm,
∴AC′=AB-BC′=4cm,
設DC=xcm,則AD=(8-x)cm,
在Rt△ADC′中,AD2=AC′2+C′D2,
即(8-x)2=x2+42,解得x=3,
∵∠AC′D=90°,
∴△ADC′的面積═![]() ×AC′×C′D=
×AC′×C′D=![]() ×4×3=6(cm2).
×4×3=6(cm2).


科目:初中數學 來源: 題型:
【題目】若兩個一次函數的圖象與x軸交于同一點,則稱這兩個函數為一對“x牽手函數”,這個交點為“x牽手點”.
(1)一次函數y=x﹣1與x軸的交點坐標為 ;一次函數y=ax+2與一次函數y=x﹣1為一對“x牽手函數”,則a= ;
(2)已知一對“x牽手函數”:y=ax+1與y=bx﹣1,其中a,b為一元二次方程x2﹣kx+k﹣4=0的兩根,求它們的“x牽手點”.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,∠BAD=60°,對角線AC、BD相交于點O將其繞著點O順時針旋轉90°得到菱形A‘B’C‘D’.若AB=1,則旋轉前后兩菱形重疊部分圖形的周長為__________
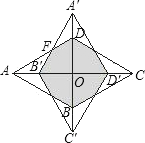
查看答案和解析>>
科目:初中數學 來源: 題型:
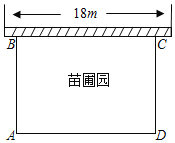
【題目】某中學課外興趣活動小組準備圍建一個矩形的苗圃圓.其中一邊靠墻,另外三邊用長為40m的籬笆圍成.已知墻長為18m(如圖所示),設這個苗圃園垂直于墻的一邊AB為xm
(1)用含有x的式子表示AD,并寫出x的取值范圍;
(2)若苗圃園的面積為192m2平方米,求AB的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
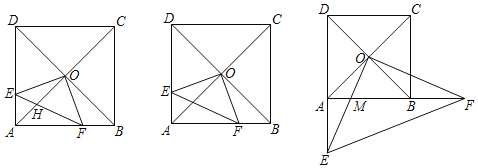
【題目】已知正方形ABCD,對角線AC、BD交于點O,線段OE⊥OF,且與邊AD、AB交于點E、F.
(1)求證:OE=OF;
(2)連接EF,交AC于點H,若HF:AF=![]() :2,求OH:EF;
:2,求OH:EF;
(3)若E、F分別在DA、AB延長線上,OE與AB交于點M,若△MOF∽△EAF,AF=1,求正方形ABCD的邊長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若中學生體質健康綜合評定成績為x分,滿分為100分.規定:85≤x≤100為A級,75≤x<85為B級,60≤x<75為C級,x<60為D級.現隨機抽取某中學部分學生的綜合評定成績,整理繪制成如下兩幅不完整的統計圖.
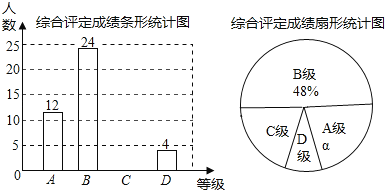
請根據圖中的信息,解答下列問題:
(1)在這次調查中,一共抽取了 名學生;a= %;C級對應的圓心角為 度.
(2)補全條形統計圖;
(3)若該校共有2000名學生,請你估計該校D級學生有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,在一個不透明的口袋中有4個形狀、大小、材質完全相同的球,其中1個紅色球,3個黃色球.
(1)從口袋中隨機取出一個球(不放回),接著再取出一個球,請用樹形圖或列表的方法求取出的兩個球一個是紅色球,一個是黃色球的概率;
(2)小明往該口袋中又放入m個紅色球和(m+2)個黃色球,再從口袋中隨機取出一個球,這個球是黃色球的概率為![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
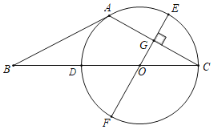
【題目】如圖,在△ABC中,AB=AC,∠BAC=120°,點O在BC上,⊙O經過點A,點C,且交BC于點D,直徑EF⊥AC于點G.
(1)求證:AB是⊙O的切線;
(2)若AC=8,求BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC內接于⊙O,∠B=600,CD是⊙O的直徑,點P是CD延長線上的一點,且AP=AC.
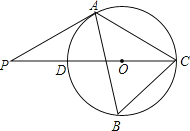
(1)求證:PA是⊙O的切線;
(2)若PD=![]() ,求⊙O的直徑.
,求⊙O的直徑.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com