【題目】如圖，在平行四邊形ABCD中，AB＝AE．若AE平分∠DAB，∠EAC＝25°，則∠B＝_____，∠AED的度數為_____．
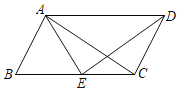
【答案】60° 85°
【解析】
先證△ABC≌△EAD（SAS），得出∠BAC＝∠AED，再證△ABE為等邊三角形．得出∠B＝∠BAE＝60°，求出∠BAC＝85°，即可得出答案．
解：∵四邊形ABCD為平行四邊形，
∴AD∥BC，AD＝BC．
∴∠DAE＝∠AEB．
∵AB＝AE，
∴∠AEB＝∠B．
∴∠B＝∠DAE．
∵在△ABC和△EAD中，
，
∴△ABC≌△EAD（SAS），
∴∠BAC＝∠AED，
∵AE平分∠DAB，
∴∠DAE＝∠BAE；
又∵∠DAE＝∠AEB，
∴∠BAE＝∠AEB＝∠B．
∴△ABE為等邊三角形．
∴∠B＝∠BAE＝60°，
∵∠EAC＝25°，
∴∠BAC＝85°，
∴∠AED＝85°．
故答案為：60°，85°．
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，拋物線
的解析式為
，將拋物線沿
軸翻折得到拋物線
，拋物線、的頂點分別為
、
，點
為拋物線上一點，橫坐標為
，過點作軸的平行線交拋物線于點
．
（1）當
時；
①請直接寫出拋物線的解析式；
②當
時，求
的值；
（2）當
時．
①
為拋物線上一動點，當
為等腰直角三角形時，求
的值；
②以
為邊向左作正方形
，設橫坐標為整數的點稱為“夢想點”，當正方形的內部（不包括邊上）有6個“夢想點”時，直接寫出的取值范圍．
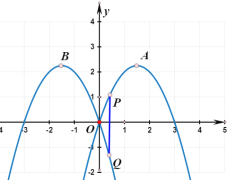
查看答案和解析>>
科目：初中數學 來源： 題型：
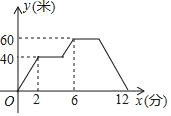
【題目】小明在練習操控航拍無人機，該型號無人機在上升和下落時的速度相同，設無人機的飛行高度為y（米），小明操控無人飛機的時間為x（分），y與x之間的函數圖象如圖所示．
（1）無人機上升的速度為 米/分，無人機在40米的高度上飛行了 分．
（2）求無人機下落過程中，y與x之間的函數關系式．
（3）求無人機距地面的高度為50米時x的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，將拋物線
向右平移
個單位，再向上平移個單位，得到拋物線
，直線
與
的一個交點記為
，與的一個交點記為
，點的橫坐標是
，點在第一象限內．
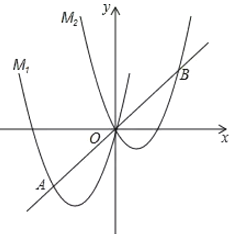
（1）求點的坐標及的表達式；
（2）點
是線段
上的一個動點，過點作
軸的垂線，垂足為
，在
的右側作正方形
．
①當點的橫坐標為
時，直線
恰好經過正方形的頂點
，求此時
的值；
②在點的運動過程中，若直線與正方形始終沒有公共點，直接寫出的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】“端午節”是我國的傳統佳節，民間歷來有吃“粽子”的習俗．我市某食品廠為了解市民對去年銷量較好的肉餡粽、豆沙餡粽、紅棗餡粽、蛋黃餡粽（以下分別用A，B，C，D表示）這四種不同口味粽子的喜愛情況，在節前對某居民區市民進行了抽樣調查，并將調查情況繪制成如下兩幅統計圖
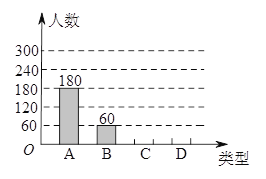
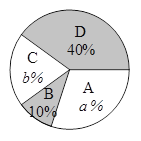
請根據以上信息回答：
（1）本次參加抽樣調查的居民有________人；
（2）扇形統計圖中：a=________，b=_________，并把條形統計圖補充完整；
（3）若有外型完全相同的A，B，C，D粽各一個，煮熟后，小王吃了兩個，用列表或畫樹狀圖的方法，求他第二個吃到的恰好是C粽的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某客商準備采購一批特色商品，經調查，用16000元采購A型商品的件數是用7500元采購B型商品的件數的2倍，一件A型商品的進價比一件B型商品的進價多10元．
（1）求一件A，B型商品的進價分別為多少元？
（2）若該客商購進A，B型商品共250件進行試銷，其中A型品的件數不大于B型商品的件數，且不小于80件，已知A型商品的售價為240元/件，B型商品的售價為220元/件，且全部售出，設購進A型商品m件，求該客商銷售這批商品的利潤y與m之間的函數關系式，并寫出m的取值范圍；
（3）在（2）的條件下，客商決定在試銷活動中每售出一件A型商品，就從一件A型商品的利潤中捐獻慈善資金a元（0＜a＜80），若該客商售完所有商品并捐獻資金后獲得的最大收益是17100元，求的a值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，
為坐標原點，拋物線
交
軸于點
，交
軸于點
．
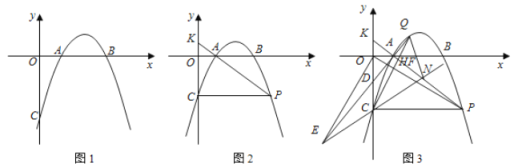
（1）如圖1，求拋物線的解析式；
（2）如圖2，點
為拋物線上一點，連接
并延長交軸于點
，若點的橫坐標為4，求
的面積；
（3）如圖3，點為對稱軸右側第四象限拋物線上一點，連接并延長交軸于點，過點
作
交軸于點
．連接
，過點作
交
延長線于點
，當
時，延長
交拋物線于點
，點
在直線
上，連接
，交線段
于點
，將射線繞點逆時針旋轉45°，得到射線
交線段于點
，交直線于點
，若
，求
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：⊙O1與⊙O2相交于A、B兩點，且O2在⊙O1上．
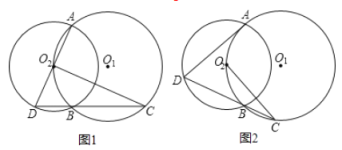
（1）如圖1，AD是⊙O2的直徑，連DB并延長交⊙O1于點C，求證：CO2⊥AD．
（2）如圖2，若AD是⊙O2的非直徑的弦，直線DB交⊙O1于點C，則(1)中的結論是否成立，為什么？請加以證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了了解市民“獲取新聞的最主要途徑”某市記者開展了一次抽樣調查，根據調查結果繪制了如下尚不完整的統計圖．
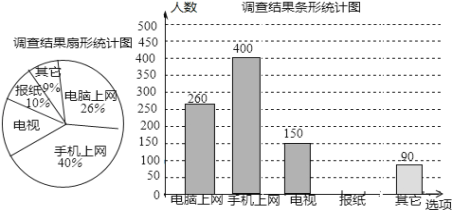
根據以上信息解答下列問題：
（1）這次接受調查的市民總人數是 ；請補全條形統計圖；
（2）扇形統計圖中，“電視”所對應的圓心角的度數是 ；
（3）若該市約有90萬人，請你估計其中將“電腦和手機上網”作為“獲取新聞的最主要途徑”的總人數。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com