
【題目】如圖,將拋物線![]() 向右平移
向右平移![]() 個單位,再向上平移
個單位,再向上平移![]() 個單位,得到拋物線
個單位,得到拋物線![]() ,直線
,直線![]() 與
與![]() 的一個交點記為
的一個交點記為![]() ,與
,與![]() 的一個交點記為
的一個交點記為![]() ,點
,點![]() 的橫坐標是
的橫坐標是![]() ,點
,點![]() 在第一象限內.
在第一象限內.
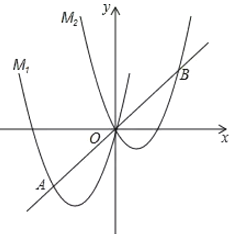
(1)求點![]() 的坐標及
的坐標及![]() 的表達式;
的表達式;
(2)點![]() 是線段
是線段![]() 上的一個動點,過點
上的一個動點,過點![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() ,在
,在![]() 的右側作正方形
的右側作正方形![]() .
.
①當點![]() 的橫坐標為
的橫坐標為![]() 時,直線
時,直線![]() 恰好經過正方形
恰好經過正方形![]() 的頂點
的頂點![]() ,求此時
,求此時![]() 的值;
的值;
②在點![]() 的運動過程中,若直線
的運動過程中,若直線![]() 與正方形
與正方形![]() 始終沒有公共點,直接寫出
始終沒有公共點,直接寫出![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]() 或
或![]()
【解析】
(1)根據點![]() 在直線
在直線![]() ,且點
,且點![]() 的橫坐標是
的橫坐標是![]() 即可得到A的坐標,再用待定系數法求出
即可得到A的坐標,再用待定系數法求出![]() 的表達式,再根據平移法則:左加右減,上加下減即可得到
的表達式,再根據平移法則:左加右減,上加下減即可得到![]() 的表達式;
的表達式;
(2) ①根據正方形的性質,得到F的坐標,求出直線![]() 的表達式,進而可以求n;
的表達式,進而可以求n;
②根據題目條件直接寫出即可;
(1)因為點![]() 在直線
在直線![]() ,且點
,且點![]() 的橫坐標是
的橫坐標是![]() ,所以
,所以![]() .
.
把![]() 代入
代入![]() ,
,
解得![]() .
.
所以![]() ,故頂點為
,故頂點為![]() .
.
將拋物線![]() 向右平移
向右平移![]() 個單位,再向上平移
個單位,再向上平移![]() 個單位,得到拋物線
個單位,得到拋物線![]() ,
,
∴![]() :
:![]() ,
,
所以![]() 的表達式為
的表達式為![]() .
.
(2)如圖:
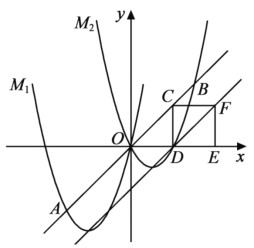
①由題意,![]() ,
,
∵四邊形CDEF是正方形,
所以![]() ,
,
因為直線![]() 經過點
經過點![]() ,所以
,所以![]() .解得
.解得![]() .
.
②解:根據題意可得,點C在A點或者B點時正方形![]() 的面積最大,
的面積最大,
又∵![]() ,
,![]()
直線![]() 與正方形
與正方形![]() 始終沒有公共點,
始終沒有公共點,
如圖,是有交點的臨界條件,
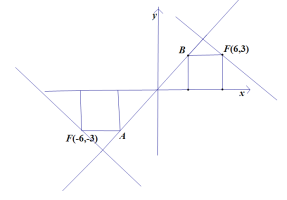
則要沒有交點,即:![]() ,或者
,或者![]()
解得:![]() 或
或 ![]() ,
,
故結果為:![]() ,
,![]() .
.


科目:初中數學 來源: 題型:
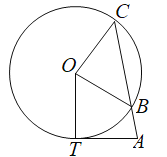
【題目】如圖,已知AT切圓O于點T,點B在圓O上,且![]() ,連接AB并延長交圓O于點C,圓O的半徑為2,若AT的長恰好為2.
,連接AB并延長交圓O于點C,圓O的半徑為2,若AT的長恰好為2.
(1)求證:△BOC是等腰直角三角形;
(2)求AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC,以AB為直徑的⊙O分別交AC、BC于點D、F,連接BD交OF于點E.
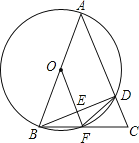
(1)求證:OF⊥BD;
(2)若AB=![]() ,DF=
,DF=![]() ,求AD的長.
,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近日,某中學舉辦了一次以“弘揚傳統文化”為主題的漢字聽寫比賽,初一和初二兩個年級各有600名學生參加,為了更好地了解本次比賽成績的分布情況,學校分別從兩個年級隨機抽取了若干名學生的成績作為樣本進行分析,下面是初二年級學生成績樣本的頻數分布表和頻數分布直方圖(不完整,每組分數段中的分數包括最低分,不包括最高分)
初二學生樣本成績頻數分布表 | ||
分組/分 | 頻數 | 頻率 |
50~60 | 2 | |
60~70 | 4 | 0.10 |
70~80 | 0.20 | |
80~90 | 14 | 0.35 |
90~100 | ||
合計 | 40 | 1.00 |
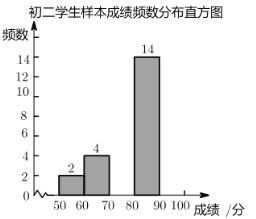
請根據所給信息,解答下列問題:
(1)補全成績頻數分布表和頻數分布直方圖.
(2)若初二學生成績樣本中80~90分段的具體成績為:
80 80 81.5 82 82.5 82.5 83 84.5 85 86.5 87 88 88.5 89
①根據上述信息,估計初二學生成績的中位數為__________.
②若初一學生樣本成績的中位數為80,甲同學在比賽中得到了82分,在他所在的年級中位居275名,根據上述信息推斷甲同學所在年級為__________(選填“初一”或者“初二”).
③若成績在85分及以上均為“優秀”,請你根據抽取的樣本數據,估計初二年級學生中達到“優秀”的學生人數為__________人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,函數y![]() (x>0)的圖象與直線y=2x+1交于點A(1,m)
(x>0)的圖象與直線y=2x+1交于點A(1,m)
(1)求k,m的值;
(2)已知點P(0,n)(n>0),過點P作平行于x軸的直線,交直線y=2x+1于點B,交函數y![]() (x>0)的圖象于點C.橫、縱坐標都是整數的點叫做整點.
(x>0)的圖象于點C.橫、縱坐標都是整數的點叫做整點.
①當n=1時,寫出線段BC上的整點的坐標;
②若y![]() (x>0)的圖象在點A,C之間的部分與線段AB,BC所圍成的區域內(包括邊界)恰有6個整點,直接寫出n的取值范圍.
(x>0)的圖象在點A,C之間的部分與線段AB,BC所圍成的區域內(包括邊界)恰有6個整點,直接寫出n的取值范圍.
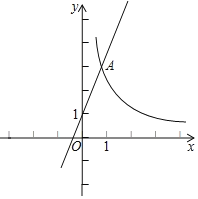
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點(點
兩點(點![]() 在點
在點![]() 左側),與
左側),與![]() 軸交于點
軸交于點![]() 的面積為
的面積為![]() .動點
.動點![]() 從點
從點![]() 出發沿
出發沿![]() 方向以每秒
方向以每秒![]() 個單位的速度向點
個單位的速度向點![]() 運動,過
運動,過![]() 作
作![]() 軸交
軸交![]() 于
于![]() .交拋物線于
.交拋物線于![]() .
.

![]() 求拋物線的解析式.
求拋物線的解析式.
![]() 當
當![]() 最大時,求運動的時間.
最大時,求運動的時間.
![]() 經過多長時間,點
經過多長時間,點![]() 到點
到點![]() 、點
、點![]() 的距離相等?
的距離相等?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在菱形ABCD中,對角線AC與BD相交于點O,AB=13,BD=24,在菱形ABCD的外部以AB為邊作等邊三角形 ABE.點F是對角線BD上一動點(點F不與點B重合),將線段AF繞點A順時針方向旋轉60°得到線段AM,連接FM.
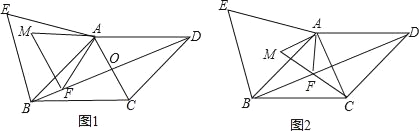
(1)求AO的長;
(2)如圖2,當點F在線段BO上,且點M,F,C三點在同一條直線上時,求證:AC=![]() AM;
AM;
(3)連接EM,若△AEM的面積為40,請直接寫出△AFM的周長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com