
【題目】某超市銷售有甲、乙兩種商品,甲商品每件進價10元,售價15元;乙商品每件進價30元,售價40元.
(1)若該超市一次性購進兩種商品共60件,且恰好用去1600元,問購進甲、乙兩種商品各多少件?
(2)若該超市要使兩種商品共60件的購進費用不超過1240元,且總利潤(利潤=售價-進價)不少于450元,請你幫助該超市設計相應的進貨方案,并指出使該超市利潤最大的方案.
【答案】(1)超市購進甲10件,購進乙商品50件;(2)見解析.
【解析】
(1)設該超市購進甲商品x件,則購進乙商品(60-x)件,根據恰好用去1600元,列出方程求出x的值,即可得到結果;
(2)設該超市購進甲商品a件,乙商品(60-a)件,根據兩種商品共60件的購進費用不超過1240元,且總利潤(利潤=售價-進價)不少于450元列出不等式組,求出不等式組的解集確定出a的值,即可設計相應的進貨方案,并找出使該超市利潤最大的方案.
(1)設超市購進甲x件,購進乙商品(60-x)件;
10x+30(60-x)=1600,
解得x=10;
購進乙商品:60-x=50
則超市購進甲商品10件,購進乙商品50件;
(2)設該超市購進甲商品a件
![]() ,
,
解得28≤a≤30.
∵a為非負整數,
所以a=28,29,30.相應的,60-a=32,31,30。
故有三種方案:
方案一:購進甲商品28件,購進乙商品32件,所獲利潤為28×5+32×10=460元;
方案二:購進甲商品29件,購進乙商品31件,所獲利潤為29×5+31×10=455元;
方案三:購進甲商品30件,購進乙商品30件,所獲利潤為30×5+30×10=450元;
所以使該超市利潤最大的方案是方案一,即購進甲商品28件,購進乙商品32件,所獲利潤為460元。


 百年學典課時學練測系列答案
百年學典課時學練測系列答案科目:初中數學 來源: 題型:
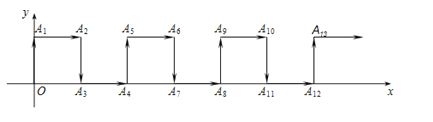
【題目】如圖,在平面直角坐標系中,一動點從原點![]() 出發,按向上.向右.向下.向右的方向依次平移,每次移動一個單位,得到
出發,按向上.向右.向下.向右的方向依次平移,每次移動一個單位,得到![]() (0,1),
(0,1),![]() (1,1),
(1,1),![]() (1,0),
(1,0),![]() (2,0),…那么點
(2,0),…那么點![]() 的坐標為__________.
的坐標為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AD平分∠CAB,交CB于點D,過點D作DE⊥AB,于點E

(1)求證:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的長。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】滿足下列條件的△ABC不是直角三角形的是()
A. BC=1,AC=2,AB=![]()
B. BC=1,AC=2,AB=![]()
C. BC:AC:AB=3:4:5
D. ∠A:∠B:∠C=3:4:5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 的圖象如圖所示,有下列結論:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正確的結論有______.
的圖象如圖所示,有下列結論:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正確的結論有______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水果批發商場經銷一種高檔水果,如果每千克盈利10元,每天可售出500千克,經市場調查發現,在進貨價不變的情況下,若每千克漲價1元,日銷量減少20千克。
(1)如果該商場要保證每天盈利6000元,同時又要使顧客得到實惠,那么每千克應漲價多少元?
(2)當每千克漲價多少元時,該商場的每天盈利最大?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,反比例函數y=kx-1(x>0)的圖象經過點A(1,2)和點B(m,n)(m>1),過點B作y軸的垂線,垂足為C.
(1)求該反比例函數解析式;
(2)當△ABC面積為2時,求點B的坐標.
(3)P為線段AB上一動點(P不與A、B重合),在(2)的情況下,直線y=ax﹣1與線段AB交于點P,直接寫出a的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
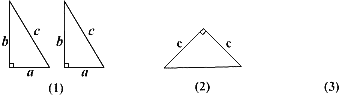
【題目】如圖(1)是用硬紙板做成的兩個全等的直角三角形,兩直角邊的長分別為![]() 和
和![]() 斜邊長為
斜邊長為![]() 圖(2)是以
圖(2)是以![]() 為直角邊的等腰直角三角形.請你開動腦筋,將它們拼成一個直角梯形.
為直角邊的等腰直角三角形.請你開動腦筋,將它們拼成一個直角梯形.
(1)在圖(3)處畫出拼成的這個圖形的示意圖;
(2)利用(1)畫出的圖形證明勾股定理.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com