
【題目】如圖,一次函數y=﹣2x+4的圖象與x軸、y軸分別交于點A、B,點C是OA的中點,過點C作CD⊥OA于C交一次函數圖象于點D,P是OB上一動點,則PC+PD的最小值為( )

A.4B.![]() C.2
C.2![]() D.2
D.2![]() +2
+2
【答案】C
【解析】
作點C關于y軸的對稱點C′,連接C′D交y軸于點P,此時PC+PD取得最小值,利用一次函數圖象上點的坐標特征可得出點A的坐標,由點C是OA的中點可得出點C的坐標,由點C,C′關于y軸對稱可得出CC′的值及PC=PC′,再利用勾股定理即可求出此時C′D(即PC+PD)的值,此題得解.
解:作點C關于y軸的對稱點C′,連接C′D交y軸于點P,此時PC+PD取得最小值,如圖所示.
當y=0時,﹣2x+4=0,解得:x=2,
∴點A的坐標為(2,0).
∵點C是OA的中點,
∴OC=1,點C的坐標為(1,0).
當x=1時,y=﹣2x+4=2,
∴CD=2.
∵點C,C′關于y軸對稱,
∴CC′=2OC=2,PC=PC′,
∴PC+PD=PC′+PD=C′D=![]() .
.
故選:C.



 培優三好生系列答案
培優三好生系列答案 優化作業上海科技文獻出版社系列答案
優化作業上海科技文獻出版社系列答案科目:初中數學 來源: 題型:
【題目】已知:在平面直角坐標系中,![]() 為
為![]() 軸負半軸上的點,
軸負半軸上的點,![]() 為
為![]() 軸負半軸上的點.
軸負半軸上的點.
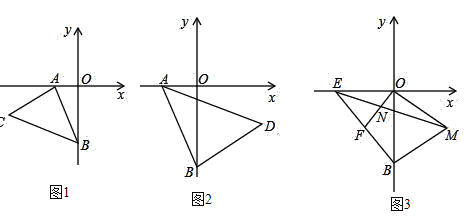
(1)如圖1,以![]() 點為頂點、
點為頂點、![]() 為腰在第三象限作等腰
為腰在第三象限作等腰![]() ,若
,若![]() ,
,![]() ,試求
,試求![]() 點的坐標;
點的坐標;
(2)如圖![]() ,若點
,若點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的縱坐標為
的縱坐標為![]() ,以
,以![]() 為頂點,
為頂點,![]() 為腰作等腰
為腰作等腰![]() .試問:當
.試問:當![]() 點沿
點沿![]() 軸負半軸向下運動且其他條件都不變時,整式
軸負半軸向下運動且其他條件都不變時,整式![]() 的值是否發生變化?若不發生變化,請求出其值;若發生變化,請說明理由;
的值是否發生變化?若不發生變化,請求出其值;若發生變化,請說明理由;
(3)如圖![]() ,
,![]() 為
為![]() 軸負半軸上的一點,且
軸負半軸上的一點,且![]() ,
,![]() 于點
于點![]() ,以
,以![]() 為邊作等邊
為邊作等邊![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() ,試探索:在線段
,試探索:在線段![]() 、
、![]() 和
和![]() 中,哪條線段等于
中,哪條線段等于![]() 與
與![]() 的差的一半?請你寫出這個等量關系,并加以證明.
的差的一半?請你寫出這個等量關系,并加以證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=3ax2+2bx+c,
(1)若a=3k,b=5k,c=k+1,試說明此類函數圖象都具有的性質;
(2)若a=![]() , c=2+b且拋物線在﹣2≤x≤2區間上的最小值是﹣3,求b的值;
, c=2+b且拋物線在﹣2≤x≤2區間上的最小值是﹣3,求b的值;
(3)若a+b+c=1,是否存在實數x,使得相應的y的值為1,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是8×8的標準點陣圖,直線l、m互相垂直,已知△ABC.

(1)寫出△ABC的形狀;
(2)分別畫出△ABC關于直線l、m對稱的△A1B1C1,△A2B2C2,再畫出△A1B1C1關于直線m對稱的△A3B3C3
(3)△A2B2C2與△A3B3C3關于哪條直線對稱? (填“直線l、m”)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b的圖象分別與反比例函數y=![]() 的圖象在第一象限交于點A(4,3),與y軸的負半軸交于點B,且OA=OB.
的圖象在第一象限交于點A(4,3),與y軸的負半軸交于點B,且OA=OB.
(1)求函數y=kx+b和y=![]() 的表達式;
的表達式;
(2)已知點C(0,5),試在該一次函數圖象上確定一點M,使得MB=MC,求此時點M的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,點D在AB上,且CD=CB,點E為BD的中點,點F為AC的中點,連結EF交CD于點M.
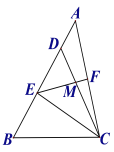
(1)求證:EF=![]() AC.
AC.
(2)連接AM,若∠BAC=45°,AM+DM=15,BE=9,求CE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P在正方形ABCD邊AD上,連接PB,過點B作一條射線與邊DC的延長線交于點 Q,使得∠QBE=∠PBC,其中E是邊AB延長線上的點,連接PQ,若PQ=PB+PD+3,則△PAB的面積為____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程解應用題:根據《中國鐵路中長期發展規劃》,預計到2020年底,我國建設城際軌道交通的公里數是客運專線的2倍。其中建設城際軌道交通約投入8000億元,客運專線約投入3500億元。據了解,建設每公里城際軌道交通與客運專線共需1.5億元。預計到2020年底,我國將建設城際軌道交通和客運專線分別約多少公里?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】利用圖象解一元二次方程x2-2x-1=0時,我們采用的一種方法是在直角坐標系中畫出拋物線y=x2和直線y=2x+1,兩圖象交點的橫坐標就是該方程的解.
(1)請再給出一種利用圖象求方程x2-2x-1=0的解的方法;
(2)已知函數y=x3的圖象(如圖),求方程x3-x-2=0的解(結果保留兩位有效數字).
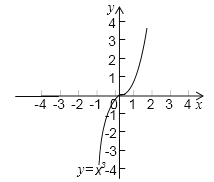
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com