
【題目】如圖1,在Rt△ABC中,∠C=90°,AC=BC=2,點D、E分別在邊AC、AB上,AD=DE=![]() AB,連接DE.將△ADE繞點A逆時針方向旋轉,記旋轉角為θ.
AB,連接DE.將△ADE繞點A逆時針方向旋轉,記旋轉角為θ.
(1)問題發現
①當θ=0°時,![]() = ;
= ;
②當θ=180°時,![]() = .
= .
(2)拓展探究
試判斷:當0°≤θ<360°時,![]() 的大小有無變化?請僅就圖2的情形給出證明;
的大小有無變化?請僅就圖2的情形給出證明;
(3)問題解決
①在旋轉過程中,BE的最大值為 ;
②當△ADE旋轉至B、D、E三點共線時,線段CD的長為 .

【答案】(1)①![]() ;(2)詳見解析;(3)①2
;(2)詳見解析;(3)①2![]() +2
+2![]() +1或
+1或![]() ﹣1.
﹣1.
【解析】分析:(1)①先判斷出DE∥CB,進而得出比例式,代值即可得出結論;
②先得出DE∥BC,即可得出,![]() ,再用比例的性質即可得出結論;
,再用比例的性質即可得出結論;
(2)先∠CAD=∠BAE,進而判斷出△ADC∽△AEB即可得出結論;
(3)分點D在BE的延長線上和點D在BE上,先利用勾股定理求出BD,再借助(2)結論即可得出CD.
詳解:(1)①當θ=0°時,
在Rt△ABC中,AC=BC=2,
∴∠A=∠B=45°,AB=2![]() ,
,
∵AD=DE=![]() AB=
AB=![]() ,
,
∴∠AED=∠A=45°,
∴∠ADE=90°,
∴DE∥CB,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案為:![]() ,
,
②當θ=180°時,如圖1,
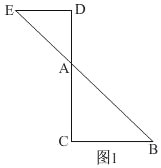
∵DE∥BC,
∴![]() ,
,
∴![]() ,
,
即:![]() ,
,
∴![]() ,
,
故答案為:![]() ;
;
(2)當0°≤θ<360°時,![]() 的大小沒有變化,
的大小沒有變化,
理由:∵∠CAB=∠DAE,
∴∠CAD=∠BAE,
∵![]() ,
,
∴△ADC∽△AEB,
∴![]() ;
;
(3)①當點E在BA的延長線時,BE最大,
在Rt△ADE中,AE=![]() AD=2,
AD=2,
∴BE最大=AB+AE=2![]() +2;
+2;
②如圖2,
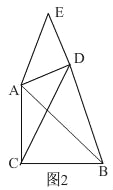
當點E在BD上時,
∵∠ADE=90°,
∴∠ADB=90°,
在Rt△ADB中,AB=2![]() ,AD=
,AD=![]() ,根據勾股定理得,BD=
,根據勾股定理得,BD=![]() =
=![]() ,
,
∴BE=BD+DE=![]() +
+![]() ,
,
由(2)知,![]() ,
,
∴CD=![]() +1,
+1,
如圖3,
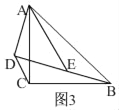
當點D在BE的延長線上時,
在Rt△ADB中,AD=![]() ,AB=2
,AB=2![]() ,根據勾股定理得,BD=
,根據勾股定理得,BD=![]() =
=![]() ,
,
∴BE=BD﹣DE=![]() ﹣
﹣![]() ,
,
由(2)知,![]() ,
,
∴CD=![]() ﹣1.
﹣1.
故答案為:![]() +1或
+1或![]() ﹣1.
﹣1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】已知y﹣2與x成正比例,當x=2時,y=6.
(1)求y與x之間的函數解析式.
(2)在所給直角坐標系中畫出函數圖象.
(3)由函數圖象直接寫出當﹣2≤y≤2時,自變量x的取值范圍.
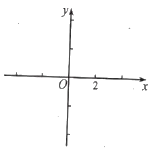
查看答案和解析>>
科目:初中數學 來源: 題型:
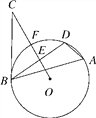
【題目】如圖,△ABD是⊙O的內接三角形,E是弦BD的中點,點C是⊙O外一點,且∠DBC=∠A,連接OE并延長與⊙O相交于點F,與BC相交于點C.
(1)求證:BC是⊙O的切線;
(2)若⊙O的半徑為6,BC=8,求弦BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店銷售10臺A型和20臺B型電腦的利潤為4000元,銷售20臺A型和10臺B型電腦的利潤為3500元.
(1)求每臺A型電腦和B型電腦的銷售利潤;
(2)該商店計劃一次購進兩種型號的電腦共100臺,其中B型電腦的進貨量不超過A型電腦的2倍,設購進A型電腦x臺,這100臺電腦的銷售總利潤為y元.
①求y關于x的函數關系式;
②該商店購進A型、B型電腦各多少臺,才能使銷售總利潤最大?
(3)實際進貨時,廠家對A型電腦出廠價下調m(0<m<100)元,且限定商店最多購進A型電腦70臺.若商店保持兩種電腦的售價不變,請你根據以上信息及(2)中條件,設計出使這100臺電腦銷售總利潤最大的進貨方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠C=90°,AC=6,BC=8,點D、E分別是斜邊AB和直角邊BC上的點,把△ABC沿著直線DE折疊,頂點B的對應點是點B′.
(1)如圖①,如果點B′和點A重合,求CE的長.
(2)如圖②,如果點B′落在直角邊AC的中點上,求BE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,□ABCD中,對角線AC與AB、AD的夾角分別為α、β,點E是AC上任意一點,給出如下結論:①AB sinα=AD sinβ;②S△ABE=S△ADE;③ADsinα=AB sinβ. 其中正確的個數有( )
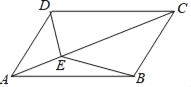
A. 0個 B. 1個 C. 2個 D. 3個
查看答案和解析>>
科目:初中數學 來源: 題型:
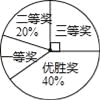
【題目】國務院辦公廳在2015年3月16日發布了《中國足球發展改革總體方案》,這是中國足球史上的重大改革,為進一步普及足球知識,傳播足球文化,我市某區在中小學舉行了“足球在身邊”知識競賽,各類獲獎學生人數的比例情況如圖所示,其中獲得三等獎的學生共50名,請結合圖中信息,解答下列問題:
(1)獲得一等獎的學生人數;
(2)在本次知識競賽活動中,A,B,C,D四所學校表現突出,現決定從這四所學校中隨機選取兩所學校舉行一場足球友誼賽,請用畫樹狀圖或列表的方法求恰好選到A,B兩所學校的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知A=3a2b-2ab2+abc,小明同學錯將“2A-B”看成“2A+B”,算得結果為4a2b-3ab2+4abc.
(1)求出2A-B的結果;
(2)小強同學說(1)中的結果的大小與c的取值無關,正確嗎?若a=![]() ,b=
,b=![]() ,求(1)中式子的值.
,求(1)中式子的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com