
【題目】在平面直角坐標系![]() 中,拋物線
中,拋物線![]() 與
與![]() 軸交于點A,將點A向右平移2個單位長度,得到點B,點B在拋物線上.
軸交于點A,將點A向右平移2個單位長度,得到點B,點B在拋物線上.
(1)求點B的坐標(用含![]() 的式子表示);
的式子表示);
(2)求拋物線的對稱軸;
(3)已知點![]() ,
,![]() .若拋物線與線段PQ恰有一個公共點,結合函數圖象,求
.若拋物線與線段PQ恰有一個公共點,結合函數圖象,求![]() 的取值范圍.
的取值范圍.
【答案】(1)點B的坐標為![]() ;(2)對稱軸為直線
;(2)對稱軸為直線![]() ;(3)當
;(3)當![]() 時,拋物線與線段PQ恰有一個公共點.
時,拋物線與線段PQ恰有一個公共點.
【解析】
(1)![]() 向右平移2個單位長度,得到點
向右平移2個單位長度,得到點![]() ;
;
(2)A與B關于對稱軸x=1對稱;
(3))①a>0時,當x=2時,![]() ,當
,當![]() 時,x=0或x=2,所以函數與AB無交點;②a<0時,當y=2時,
時,x=0或x=2,所以函數與AB無交點;②a<0時,當y=2時,![]() ,
,![]() 或
或![]() 當
當![]() 時,
時,![]() ;
;
解:(1)∵拋物線與![]() 軸交于點A,∴令
軸交于點A,∴令![]() ,得
,得![]() ,
,
∴點A的坐標為![]() ,∵點A向右平移兩個單位長度,得到點B,
,∵點A向右平移兩個單位長度,得到點B,
∴點B的坐標為![]() ;
;
(2)∵拋物線過點![]() 和點
和點![]() ,由對稱性可得,拋物線對稱軸為
,由對稱性可得,拋物線對稱軸為
直線![]() ,故對稱軸為直線
,故對稱軸為直線![]()
(3)∵對稱軸x=1,
∴b-2a,![]() ,
,
①a>0時,
當x=2時,![]() ,當
,當![]() x=0或x=2,
x=0或x=2,
∴函數與AB無交點;
②a<0時,
當y=2時,![]() ,
,
![]() 或
或![]() 當
當![]() 時,
時,![]() ;
;
∴當![]() 時,拋物線與線段PQ恰有一個公共點;
時,拋物線與線段PQ恰有一個公共點;
(3)①當![]() 時,則
時,則![]() ,分析圖象可得:根據拋物線的對稱性,拋物線不可能同時經過點A和點P;也不可能同時經過點B和點Q,所以,此時線段PQ與拋物線沒有交點.
,分析圖象可得:根據拋物線的對稱性,拋物線不可能同時經過點A和點P;也不可能同時經過點B和點Q,所以,此時線段PQ與拋物線沒有交點.
②當![]() 時,則
時,則![]() .
.
分析圖象可得:根據拋物線的對稱性,拋物線不可能同時經過點A和點P;但當點Q在點B上方或與點B重合時,拋物線與線段PQ恰有一個公共點,此時![]() 即
即
![]()
綜上所述,當![]() 時,拋物線與線段PQ恰有一個公共點.
時,拋物線與線段PQ恰有一個公共點.


 捷徑訓練檢測卷系列答案
捷徑訓練檢測卷系列答案 小夫子全能檢測系列答案
小夫子全能檢測系列答案科目:初中數學 來源: 題型:
【題目】湘潭市繼2017年成功創建全國文明城市之后,又準備爭創全國衛生城市.某小區積極響應,決定在小區內安裝垃圾分類的溫馨提示牌和垃圾箱,若購買2個溫馨提示牌和3個垃圾箱共需550元,且垃圾箱的單價是溫馨提示牌單價的3倍.
(1)求溫馨提示牌和垃圾箱的單價各是多少元?
(2)該小區至少需要安放48個垃圾箱,如果購買溫馨提示牌和垃圾箱共100個,且費用不超過10000元,請你列舉出所有購買方案,并指出哪種方案所需資金最少?最少是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中, ![]() , 在
, 在![]() ,上取一點
,上取一點![]() ,以
,以![]() 為直徑作
為直徑作![]() ,與
,與![]() 相交于點
相交于點![]() ,作線段
,作線段![]() 的垂直平分線
的垂直平分線![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() .
.
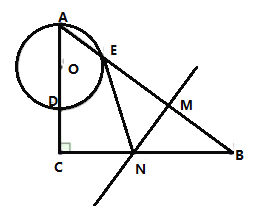
(1) 求證:![]() 是
是![]() 的切線;
的切線;
(2)若![]() ,
,![]() 的半徑為
的半徑為![]() .求線段
.求線段![]() 與線段
與線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y= x2-4x+3.
(1)把這個二次函數化成![]() 的形式并寫出拋物線的頂點坐標;
的形式并寫出拋物線的頂點坐標;
(2)畫出這個二次函數的圖象,并利用圖象直接寫出當y>0時,x的取值范圍. 當x取何值時,y隨x的增大而減小;
(3)若拋物線與![]() 軸的交點記為A,B,該圖象上存在一點C,且△ABC的面積為3,求點C的坐標.
軸的交點記為A,B,該圖象上存在一點C,且△ABC的面積為3,求點C的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
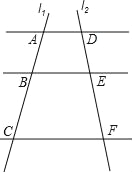
【題目】如圖,已知AD∥BE∥CF,它們依次交直線l1、l2于點A、B、C和點D、E、F,![]() ,AC=14;
,AC=14;
(1)求AB、BC的長;
(2)如果AD=7,CF=14,求BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某單位準備組織員工到武夷山風景區旅游,旅行社給出了如下收費標準(如圖所示):

設參加旅游的員工人數為x人.
(1)當25<x<40時,人均費用為 元,當x≥40時,人均費用為 元;
(2)該單位共支付給旅行社旅游費用27000元,請問這次參加旅游的員工人數共有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() =ax2+bx+c的部分對應值如表,利用二次的數的圖象可知,當函數值y>0時,x的取值范圍是( )
=ax2+bx+c的部分對應值如表,利用二次的數的圖象可知,當函數值y>0時,x的取值范圍是( )
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 |
y | ﹣12 | ﹣5 | 0 | 3 | 4 | 3 |
A.0<x<2B.x<0或x>2C.﹣1<x<3D.x<﹣1或x>3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=ax2+bx+c的頂點為D(﹣1,2),與x軸的一個交點A在點(﹣3,0)和(﹣2,0)之間,其部分圖象如圖,則以下結論:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有兩個相等的實數根.其中正確結論的個數為( )
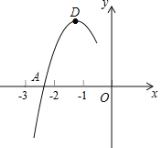
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com