
 AD上以每秒2個單位的速度向點D移動.當點F與點D重合時,E、F兩點同時停止移動.設點E移動時間為t秒.
AD上以每秒2個單位的速度向點D移動.當點F與點D重合時,E、F兩點同時停止移動.設點E移動時間為t秒. =
=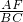 即:
即: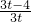 =
= ;解得t2-6t+8=0,t1=2,t2=4
;解得t2-6t+8=0,t1=2,t2=4 時,S=
時,S= (2t+12)×4-
(2t+12)×4- (4-3t)×2t=3t2+24;
(4-3t)×2t=3t2+24; ≤t≤4時,S=
≤t≤4時,S= (2t+12)×4+12(3t-4)×2t=3t2+24
(2t+12)×4+12(3t-4)×2t=3t2+24  =1.
=1. ,t2=3+
,t2=3+ (舍去);
(舍去); (舍去負值);
(舍去負值); (舍去),t2=3+
(舍去),t2=3+ ;
; ,
, ,
, ,3+
,3+ ,
, 秒時,以B、E、F為頂點的三角形是等腰三角形.
秒時,以B、E、F為頂點的三角形是等腰三角形.

 優百分課時互動系列答案
優百分課時互動系列答案科目:初中數學 來源: 題型:
 如圖,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,cosC=
如圖,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,cosC=
| ||
| 10 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com