
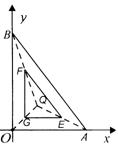
我們把三角形內部的一個點到這個三角形三邊所在直線距離的最小值叫做這個點到這個三角形的距離.如圖1,PD⊥BC于D,PE⊥AC于![]() E,PF⊥AB于F,如果PE≥PF≥PD,則稱PD的長度為點P到△ABC的距離.
E,PF⊥AB于F,如果PE≥PF≥PD,則稱PD的長度為點P到△ABC的距離.
在圖2、圖3中,已知A(6,0),B(0,8).
(1)若圖2中點P的坐標為(2,4),求 P到△AOB的距離;
(2)若點R是圖3中△AOB內一點,且點R到△AOB的距離為1,請在圖3中畫出滿足條件的點R所構成的封閉圖形,并求出這個圖形的周長.
 |
(1) ∵A(6,0),B(0,8)∴OA=6,OB=8,在Rt△AOB中,AB=10…………(1分)
過點P分別作PC⊥OA、 PD⊥OB、 PE⊥AB,垂足分別為C、D、E
 ∵S△POB +S△PAB +S△POA =S△ABO
∵S△POB +S△PAB +S△POA =S△ABO
∴![]()
∴PE=0.8…………………………… (3分)
∴P到△AOB的距離為0.8………………………… (4分)
(2)設點Q為△AOB的內心,連接QA,QB,QO,分別取QA,QB,QO 的中點E,F,G![]() ,連接EF,FG,GE,則△EFG即為所要畫的圖形. …………… (6分)
,連接EF,FG,GE,則△EFG即為所要畫的圖形. …………… (6分)
由畫圖可知,△EFG∽△ABO,由上題及已知條件可知,△EFG與△ABO的相似比為![]() ,因為△ABO的周長為24,所以△EFG的周長為12.……………
,因為△ABO的周長為24,所以△EFG的周長為12.……………![]() ………(9分)
………(9分)


科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:

| AB |
| DC |
| BE |
| EC |
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com