
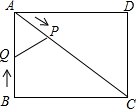
 如圖,在矩形ABCD中,AB=3,BC=4.動點P從點A出發沿AC向終點C運動,同時動點Q從點B出發沿BA向點A運動,到達A點后立刻以原來的速度沿AB返回.點P,Q運動速度均為每秒1個單位長度,當點P到達點C時停止運動,點Q也同時停止.連結PQ,設運動時間為t(t>0)秒.
如圖,在矩形ABCD中,AB=3,BC=4.動點P從點A出發沿AC向終點C運動,同時動點Q從點B出發沿BA向點A運動,到達A點后立刻以原來的速度沿AB返回.點P,Q運動速度均為每秒1個單位長度,當點P到達點C時停止運動,點Q也同時停止.連結PQ,設運動時間為t(t>0)秒.分析 (1)①由勾股定理求出AC,再證明△APQ∽△ABC,得出對應邊成比例,即可得出結果;
②過點P作PH⊥AB于點H,AP=t,AQ=3-t,證△AHP∽△ABC,求出PH=$\frac{4}{5}$t,根據三角形面積公式求出即可;
(2)①根據線段的垂直平分線的性質求出AP=AQ,得出3-t=t,求出即可,延長QP交AD于點E,過點Q作QO∥AD交AC于點O,證△AQO∽△ABC,求出AO,QO,PO=1,證△APE∽△OPQ求出AE即可;
②(ⅰ)當點Q從B向A運動時l經過點B,求出CP=AP=$\frac{1}{2}$AC=2.5,即可求出t;
(ⅱ)當點Q從A向B運動時l經過點B,求出BP=BQ=6-t,AP=t,PC=5-t,過點P作PG⊥CB于點G,證△PGC∽△ABC,求出PG=$\frac{3}{5}$(5-t),CG=$\frac{4}{5}$(5-t),BG=$\frac{4}{5}$t,由勾股定理得出方程,求出方程的解即可.
解答 解:(1)①∵四邊形ABCD是矩形,
∴∠B=90°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵PQ⊥AC,
∴∠APQ=90°=∠B,
又∵∠PAQ=∠BAC,
∴△APQ∽△ABC,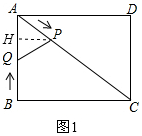
∴$\frac{AP}{AB}=\frac{AQ}{AC}$,
即$\frac{t}{3}=\frac{3-t}{5}$,
解得:t=$\frac{9}{8}$,
即t=$\frac{9}{8}$時,PQ⊥AC,
故答案為:$\frac{9}{8}$;
②如圖1所示,過點P作PH⊥AB于點H,AP=t,AQ=3-t,
則∠AHP=∠ABC=90°,
∵∠PAH=∠CAB,
∴△AHP∽△ABC,
∴$\frac{AP}{AC}=\frac{PH}{BC}$,
∵AP=t,AC=5,BC=4,
∴PH=$\frac{4}{5}$t,
∴S=$\frac{1}{2}$•(3-t)•$\frac{4}{5}$t,
即S=-$\frac{2}{5}$t2+$\frac{6}{5}$t,t的取值范圍是:0<t<3.
(2)①如圖2,線段PQ的垂直平分線為l經過點A,則AP=AQ,
即3-t=t,
∴t=1.5,
∴AP=AQ=1.5;
延長QP交AD于點E,過點Q作QO∥AD交AC于點O,
則△AQO∽△ABC,
∴$\frac{AO}{AC}=\frac{AQ}{AB}=\frac{QO}{BC}$,
∴AO=$\frac{AQ}{AB}$•AC=$\frac{5}{2}$,QO=$\frac{AQ}{AB}$•BC=2,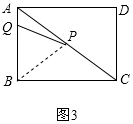
∴PO=AO-AP=1.
∵OQ∥BC∥AD,
∴△APE∽△OPQ
∴$\frac{AE}{QO}=\frac{AP}{QP}$,
∴AE=$\frac{AP}{QP}$•QO=3.
②(ⅰ)如圖3,當點Q從B向A運動時l經過點B,
BQ=CP=AP=t,∠QBP=∠QAP
∵∠QBP+∠PBC=90°,∠QAP+∠PCB=90°
∴∠PBC=∠PCB CP=BP=AP=t
∴CP=AP=$\frac{1}{2}$AC=$\frac{1}{2}$×5=2.5∴t=2.5.
(ⅱ)如圖4,當點Q從A向B運動時l經過點B;
BP=BQ=3-(t-3)=6-t,AP=t,PC=5-t,
過點P作PG⊥CB于點G,則PG∥AB,
∴△PGC∽△ABC,
∴$\frac{PC}{AC}=\frac{PG}{AB}=\frac{GC}{BC}$,
∴PG=$\frac{PC}{AC}$•AB=$\frac{3}{5}$(5-t),CG=$\frac{PC}{AC}$•BC=$\frac{4}{5}$(5-t),
∴BG=4-$\frac{4}{5}$(5-t)=$\frac{4}{5}$t,
由勾股定理得:BP2=BG2+PG2,
即(6-t)2=($\frac{4}{5}$t)2+[$\frac{3}{5}$(5-t)]2,
解得:t=$\frac{45}{14}$;
綜上所述:存在t的值,使得直線l經過點B,t的值是2.5或$\frac{45}{14}$.
點評 本題是四邊形綜合題目,考查了矩形性質,等腰三角形性質,線段垂直平分線性質,勾股定理,相似三角形的性質和判定的應用,主要考查學生分析問題和解決問題的能力,題目比較典型,但是有一定的難度.


科目:初中數學 來源: 題型:選擇題
 如圖,一農戶要建一個矩形花圃,花圃的一邊利用長為12m的住房墻,另外三邊用25m長的籬笆圍成,為方便進出,在垂直于住房墻的一邊留一個1m寬的門,花圃面積為80m2,設與墻垂直的一邊長為xm(已標注在圖中),則可以列出關于x的方程是( )
如圖,一農戶要建一個矩形花圃,花圃的一邊利用長為12m的住房墻,另外三邊用25m長的籬笆圍成,為方便進出,在垂直于住房墻的一邊留一個1m寬的門,花圃面積為80m2,設與墻垂直的一邊長為xm(已標注在圖中),則可以列出關于x的方程是( )| A. | x(26-2x)=80 | B. | x(24-2x)=80 | C. | (x-1)(26-2x)=80 | D. | x(25-2x)=80 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖:在x軸的上方,直角∠BOA繞原點O順時針方向旋轉,若∠BOA的兩邊分別與函數y=-$\frac{1}{x}$、y=$\frac{2}{x}$的圖象交于B、A兩點,則tanA=$\frac{\sqrt{2}}{2}$.
如圖:在x軸的上方,直角∠BOA繞原點O順時針方向旋轉,若∠BOA的兩邊分別與函數y=-$\frac{1}{x}$、y=$\frac{2}{x}$的圖象交于B、A兩點,則tanA=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
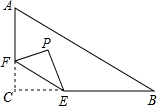 如圖,在Rt△ABC中,∠C=90°,AC=3,BC=4,點F在邊AC上,并且CF=1,點E為邊BC上的動點,將△CEF沿直線EF翻折,點C落在點P處,則點P到邊AB距離的最小值是$\frac{3}{5}$.
如圖,在Rt△ABC中,∠C=90°,AC=3,BC=4,點F在邊AC上,并且CF=1,點E為邊BC上的動點,將△CEF沿直線EF翻折,點C落在點P處,則點P到邊AB距離的最小值是$\frac{3}{5}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
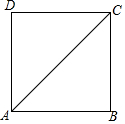 如圖,正方形ABCD的對角線AC長為2$\sqrt{2}$,若直線滿足:①點C到直線l的距離為1;②B、D兩點到直線l的距離相等,那么符合題意的直線l有4條.
如圖,正方形ABCD的對角線AC長為2$\sqrt{2}$,若直線滿足:①點C到直線l的距離為1;②B、D兩點到直線l的距離相等,那么符合題意的直線l有4條.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com