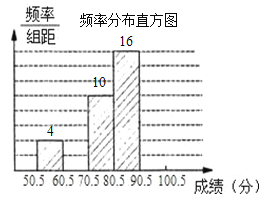
【題目】數學興趣小組成員張廣益對本年級期中考試數學成績（成績取整數，滿分為100分）做了統計分析，繪制成如下頻數、頻率分布表和頻數分布直方圖．請你根據圖表提供的信息，解答下列問題：
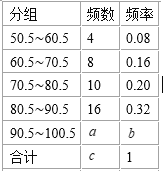
⑴填充頻率分布表中的空格：a ，b ，c ；
⑵補全頻率分布直方圖；
⑶已知本年級共計1700名學生，若競賽成績在90分以上(不含90分)為優秀，估算本年級數學成績優秀的學生約有多少人?
【答案】(1) 12,0.24,50;(2)見詳解;(3)408.
【解析】
（1）由頻數和頻率分布表的第一組數，可得隨機抽取的學生共有：頻數÷頻率=4÷0.08=50；
下面的空格中的數字運用公式：頻數÷頻率=50，求解即可；
頻數分布直方圖利用頻數和頻率分布表中的數值作圖即可．
（2）根據題中的圖和表可以看出，樣本是50名同學期中考試數學成績情況；樣本容量上一問已求出為50．
（3）若成績在90分以上（含90分）為優秀，則這隨機抽取的50個人中優秀的頻率為0.24，
所以，1700名同學的優秀率為0.24，
所以，該校成績優秀的同學為1700×0.24=408．
解：（1）解:∵4
0.08=50.
∴c=50.a=50-4-8-10-16=12
∴b=12
=0.24.
故答案為:12,0.24,50.
（2）如圖: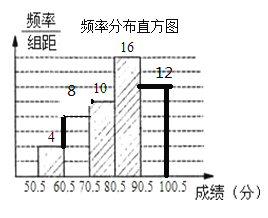 
（4）∵1700
0.24=408(人)
∴該校約有408名同學成績優秀．
科目：初中數學 來源： 題型：
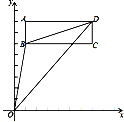
【題目】如圖，在長方形ABCD中，點A（1，8），B（1，6），C（7，6）．
(1)請直接寫出點D的坐標；
(2)連接線段OB，OD，BD，請求出△OBD的面積；
(3)若長方形ABCD以每秒1個單位長度的速度向下運動，設運動的時間為t秒，是否存在某一時刻，使△OBD的面積與長方形ABCD的面積相等？若存在，請求出t的值；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲乙兩家綠化養護公司各自推出了校園綠化養護服務的收費方案.
甲公司方案：每月的養護費用y（元）與綠化面積x（平方米）是一次函數關系，如圖所示.
乙公司方案：綠化面積不超過1000平方米時，每月收取費用5500元；綠化面積超過1000平方米時，每月在收取5500元的基礎上，超過部分每平方米收取4元.
（1）求如圖所示的y與x的函數解析式；（不要求寫取值范圍）
（2）如果某學校目前的綠化面積是1200平方米.試通過計算說明：選擇哪家公司的服務，每月的綠化養護費用較少.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，二次函數y=ax2+bx+c的圖象交x軸于A（﹣1，0），B（2，0），交y軸于C（0，﹣2），過A，C畫直線．
（1）求二次函數的解析式；
（2）點P在x軸正半軸上，且PA=PC，求OP的長；
（3）點M在二次函數圖象上，以M為圓心的圓與直線AC相切，切點為H．
①若M在y軸右側，且△CHM∽△AOC（點C與點A對應），求點M的坐標；
②若⊙M的半徑為
，求點M的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我們知道：平行四邊形的面積＝(底邊)×(這條底邊上的高)．如圖，四邊形ABCD都是平行四邊形，AD∥BC，AB∥CD，設它的面積為S．
（1）如圖①，點M為AD上任意一點，若△BCM的面積為S1，則S1：S＝ ；
（2）如圖②，點P為平行四邊形ABCD內任意一點時，記△PAB的面積為Sˊ，△PCD的面積為S〞，平行四邊形ABCD的面積為S，猜想得Sˊ、S〞的和與S的數量關系式為 ；
（3）如圖③，已知點P為平行四邊形ABCD內任意一點，△PAB的面積為3，△PBC的面積為7，求△PBD的面積．
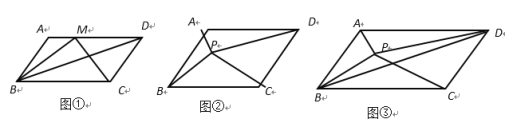
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】新知：對角線垂直的四邊形兩組對邊的平方和相等
感知與認證：如圖1，2，3中，四邊形ABCD中
于O，如圖1，AC與BD相互平分，如圖2，AC平分BD,結論顯然成立.
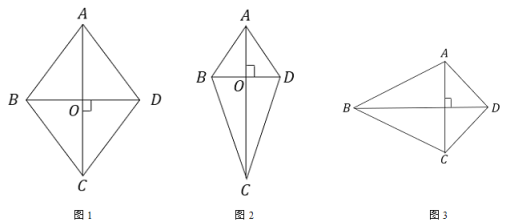
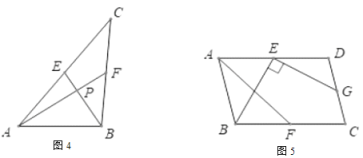
認知證明：（1）請你證明如圖3中有
成立。
發現應用：（2）如圖4，若AF,BE是三角形ABC的中線，
垂足為P
已知：
,
,求AB的長
拓展應用：（3）如圖5，在平行四邊形ABCD中，點E,F,G分別是AD,BC,CD的中點，
,
，
.求AF的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠BAC=90°，AD是中線，E是AD的中點，過點A作AF∥BC交BE的延長線于F，連接CF．
（1）求證：AD=AF；
（2）如果AB=AC，試判斷四邊形ADCF的形狀，并證明你的結論．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
