
已知:點C、A、D在同一條直線上,∠ABC=∠ADE=α,線段BD、CE交于點M.
(1)如圖1,若AB=AC,AD=AE
①問線段BD與CE有怎樣的數量關系?并說明理由;
②求∠BMC的大小(用α表示);
(2)如圖2,若AB=BC=kAC,AD=ED=kAE,則線段BD與CE的數量關系為_________,∠BMC=_________(用α表示);
(3)在(2)的條件下,把△ABC繞點A逆時針旋轉180°,在備用圖中作出旋轉后的圖形(要求:尺規作圖,不寫作法,保留作圖痕跡),連接EC并延長交BD于點M.則∠BMC=_________(用α表示).
(1)①BD=CE ②180°﹣2α (2)BD=kCE,90°﹣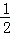 α (3)90°+
α (3)90°+ α
α
解析試題分析:(1)如圖1.
①BD=CE,理由如下:
∵AD=AE,∠ADE=α,
∴∠AED=∠ADE=α,
∴∠DAE=180°﹣2∠ADE=180°﹣2α,
同理可得:∠BAC=180°﹣2α,
∴∠DAE=∠BAC,
∴∠DAE+∠BAE=∠BAC+∠BAE,
即:∠BAD=∠CAE.
在△ABD與△ACE中,
∵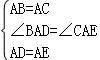 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
②∵△ABD≌△ACE,
∴∠BDA=∠CEA,
∵∠BMC=∠MCD+∠MDC,
∴∠BMC=∠MCD+∠CEA=∠DAE=180°﹣2α;
(2)如圖2.
∵AD=ED,∠ADE=α,
∴∠DAE=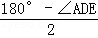 =90°﹣
=90°﹣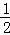 α,
α,
同理可得:∠BAC=90°﹣ α,
α,
∴∠DAE=∠BAC,
∴∠DAE+∠BAE=∠BAC+∠BAE,
即:∠BAD=∠CAE.
∵AB=kAC,AD=kAE,
∴AB:AC=AD:AE=k.
在△ABD與△ACE中,
∵AB:AC=AD:AE=k,∠BDA=∠CEA,
∴△ABD∽△ACE,
∴BD:CE=AB:AC=AD:AE=k,∠BDA=∠CEA,
∴BD=kCE;
∵∠BMC=∠MCD+∠MDC,
∴∠BMC=∠MCD+∠CEA=∠DAE=90°﹣ α.
α.
故答案為:BD=kCE,90°﹣ α;
α;
(3)如圖.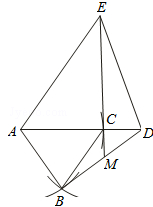
∵AD=ED,∠ADE=α,
∴∠DAE=∠AED=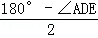 =90°﹣
=90°﹣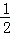 α,
α,
同理可得:∠BAC=90°﹣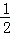 α,
α,
∴∠DAE=∠BAC,即∠BAD=∠CAE.
∵AB=kAC,AD=kAE,
∴AB:AC=AD:AE=k.
在△ABD與△ACE中,
∵AB:AC=AD:AE=k,∠BAD=∠CAE,
∴△ABD∽△ACE,
∴∠BDA=∠CEA,
∵∠BMC=∠MCD+∠MDC,∠MCD=∠CED+∠ADE=∠CED+α,
∴∠BMC=∠CED+α+∠CEA=∠AED+α=90°﹣ α+α=90°+
α+α=90°+ α.
α.
故答案為:90°+ α.
α.
考點:相似三角形的判定與性質;全等三角形的判定與性質;作圖-旋轉變換.
點評:本題考查了全等三角形的判定與性質,三角形的外角的性質,相似三角形的判定與性質,作圖﹣旋轉變換,綜合性較強,有一定難度.由于全等是相似的特殊情況,所以做第二問可以借助第一問的思路及方法,做第三問又可以遵照第二問的做法,本題三問由淺入深,層層遞進,做好第一問是關鍵.


科目:初中數學 來源: 題型:
| ||||||||
(
|
| ||||||||
(
|
| ||||||||
(
|
| 1 |
| a+b+c |
| 1 |
| b+c-a |
| 1 |
| c+a-b |
| 1 |
| c-a-b |
查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

查看答案和解析>>
科目:初中數學 來源:2013年初中數學單元提優測試卷-相似的判定解答題(解析版) 題型:解答題
已知:點C、A、D在同一條直線上,∠ABC=∠ADE=α,線段BD、CE交于點M.
(1)如圖1,若AB=AC,AD=AE
①問線段BD與CE有怎樣的數量關系?并說明理由;
②求∠BMC的大小(用α表示);
(2)如圖2,若AB=BC=kAC,AD=ED=kAE,則線段BD與CE的數量關系為 _________ ,∠BMC= _________ (用α表示);
(3)在(2)的條件下,把△ABC繞點A逆時針旋轉180°,在備用圖中作出旋轉后的圖形(要求:尺規作圖,不寫作法,保留作圖痕跡),連接EC并延長交BD于點M.則∠BMC= _________ (用α表示).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com