
如圖,直線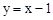 與反比例函數
與反比例函數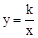 的圖象交于A、B兩點,與x軸交于點C,已知點A的坐標為(-1,m).
的圖象交于A、B兩點,與x軸交于點C,已知點A的坐標為(-1,m).
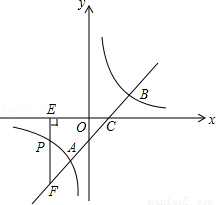
(1)求反比例函數的解析式;
(2)若點P(n,1)是反比例函數圖象上一點,過點P作PE⊥x軸于點E,延長EP交直線AB于點F,求△CEF的面積.
解:(1)將點A的坐標代入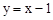 ,可得:
,可得: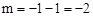 。∴點A的坐標為(-1,-2)。
。∴點A的坐標為(-1,-2)。
將點A(-1,-2)代入反比例函數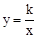 ,可得:
,可得: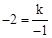 ,
,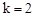 。
。
∴反比例函數解析式為: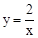 。
。
(2)將點P的縱坐標y=-1,代入反比例函數關系式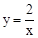 可得:x=-2,
可得:x=-2,
∴點P的坐標為(-2,-1)
將點F的橫坐標x=-2代入直線解析式可得:y=-3,∴點F的坐標為(-2,-3)。
∴EF=3,CE=OE+OC=2+1=3,∴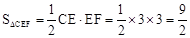 。
。
【解析】(1)將點A的坐標代入直線解析式求出m的值,再將點A的坐標代入反比例函數解析式可求出k的值,繼而得出反比例函數關系式。
(2)將點P的縱坐標代入反比例函數解析式可求出點P的橫坐標,將點P的橫坐標和點F的橫坐標相等,將點F的橫坐標代入直線解析式可求出點F的縱坐標,將點的坐標轉換為線段的長度后,即可計算△CEF的面積。


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:初中數學 來源: 題型:
 直線y=kx+b與反比例函數y=
直線y=kx+b與反比例函數y=| m | x |
查看答案和解析>>
科目:初中數學 來源: 題型:
直線![]() 與反比例函數
與反比例函數![]() 的圖象相交于點
的圖象相交于點![]() 、
、![]() ,
,
 與
與![]() 軸交于點
軸交于點![]() ,其中點
,其中點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的橫坐標為
的橫坐標為![]() .
.
(1)試確定反比例函數的關系式.
(2)求![]() 的面積.
的面積.
(3)如圖直接寫出反比例函數值大于一次函數值的自變量![]() 的取值范圍.
的取值范圍.
|
查看答案和解析>>
科目:初中數學 來源: 題型:
直線 與反比例函數
與反比例函數![]() 的圖象相交于點
的圖象相交于點![]() 、
、![]() ,
,
與 軸交于點
軸交于點![]() ,其中點
,其中點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的橫坐標為
的橫坐標為![]()
1.試確定反比例函數的關系式.
2.求![]() 的面積
的面積
3.如圖直接寫出反比例函數值大于一次函數值的自變量![]() 的取值范圍.
的取值范圍.

查看答案和解析>>
科目:初中數學 來源:《第22章 二次函數》2012年單元測試卷A(亳州市風華中學)(解析版) 題型:解答題
 (x<0)的圖象相交于點A、B,與x軸交于點C,其中點A的坐標為(-2,4),點B的橫坐標為-4.
(x<0)的圖象相交于點A、B,與x軸交于點C,其中點A的坐標為(-2,4),點B的橫坐標為-4.
查看答案和解析>>
科目:初中數學 來源:2012屆重慶一中九年級上學期開學考試數學卷 題型:填空題
直線 與反比例函數
與反比例函數 的圖象相交于點
的圖象相交于點 、
、 ,
,
 與
與 軸交于點
軸交于點 ,其中點
,其中點 的坐標為
的坐標為 ,點
,點 的橫坐標為
的橫坐標為 .
.
(1)試確定反比例函數的關系式.
(2)求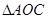 的面積.
的面積.
(3)如圖直接寫出反比例函數值大于一次函數值的自變量 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com