
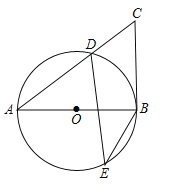
【題目】如圖,在⊙O中,AB為直徑,D.E為圓上兩點,C為圓外一點,且∠E+∠C=90°.
(1)求證:BC為⊙O的切線.
(2)若sinA=![]() ,BC=6,求⊙O的半徑.
,BC=6,求⊙O的半徑.
【答案】(1)證明見解析;(2)4.
【解析】
試題分析:(1)根據在同圓或等圓中,同弧所對的圓周角相等可得∠A=∠E,再根據三角形的內角和等于180°求出∠ABC=90°,然后根據切線的定義證明即可;
(2)根據∠A的正弦求出AC,利用勾股定理列式計算求出AB,然后求解即可.
試題解析:(1)證明:∵∠A與∠E所對的弧都是![]() ,∴∠A=∠E,又∵∠E+∠C=90°,∴∠A+∠C=90°,在△ABC中,∠ABC=180°﹣90°=90°,∵AB為直徑,∴BC為⊙O的切線;
,∴∠A=∠E,又∵∠E+∠C=90°,∴∠A+∠C=90°,在△ABC中,∠ABC=180°﹣90°=90°,∵AB為直徑,∴BC為⊙O的切線;
(2)解:∵sinA=![]() ,BC=6,∴
,BC=6,∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得AC=10,由勾股定理得,AB=
,解得AC=10,由勾股定理得,AB=![]() =
=![]() =8,∵AB為直徑,∴⊙O的半徑是
=8,∵AB為直徑,∴⊙O的半徑是![]() ×8=4.
×8=4.


科目:初中數學 來源: 題型:
【題目】某校部分住校生放學后到學校開水房打水,每人接水2升,他們先同時打開兩個放水龍頭,后來因故障關閉一個放水龍頭,假設前后兩人接水間隔時間忽略不計,且不發生潑灑,鍋爐內的余水量m(升)與接水時間t(分)的函數關系圖象如圖所示,請結合圖象,回答下列問題: 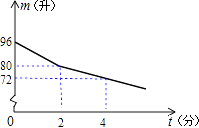
(1)請直接寫出m與t之間的函數關系式: .
(2)前15位同學接水結束共需要幾分鐘?
(3)小敏說“今天我們寢室的8位同學去開水房連續接完水恰好用了3分鐘.”你說可能嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形網格中,有格點三角形ABC(頂點都是格點)和直線MN.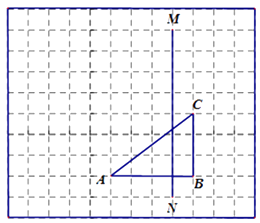
①畫出三角形ABC關于直線MN對稱的三角形 ![]()
②將三角形ABC繞點A按逆時針方向旋轉90°得到三角形 ![]() ,在正方形網格中畫出三角形
,在正方形網格中畫出三角形 ![]() 。(不要求寫作法)
。(不要求寫作法)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列調查中最適合普遍調查的是( )
A.調查某品牌燈泡的使用壽命B.調查振興區居民網上購物情況
C.調查錦江山上各種鳥的總數量D.調查我國大型客機C919的零件質量
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于反比例函數y= ![]() (k≠0),下列說法不正確的是( )
(k≠0),下列說法不正確的是( )
A.它的圖像分布在第一、三象限
B.點(k,k)在它的圖像上
C.它的圖像關于原點對稱
D.在每個象限內y隨x的增大而增大
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com