Question

如圖，在菱形ABCD中，∠A＝100°，E，F分別是邊AB和BC的中點，EP⊥CD于點P，則∠FPC＝

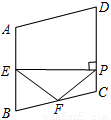
A．35°             B．45°             C．50°             D．55°

 

Answer 1

【答案】

C

【解析】

試題分析：延長EF交DC的延長線于H點．證得△BEF≌△CHF，可得EF=FH．在Rt△PEH中，利用直角三角形的性質，可得∠FPC=∠FHP=∠BEF，在等腰△BEF中即可求得求∠BEF的度數．

延長EF交DC的延長線于H點

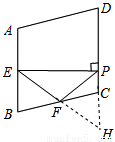
∵在菱形ABCD中，∠A=100°，E，F分別是邊AB和BC的中點

∴∠B=80°，BE=BF

∴∠BEF=（180°-80°）÷2=50°

∵AB∥DC

∴∠FHC=∠BEF=50°

又∵BF=FC，∠B=∠FCH

∴△BEF≌△CHF

∴EF=FH

∵EP⊥DC

∴∠EPH=90°

∴FP=FH

∴∠FPC=∠FHP=∠BEF=50°．

故選C．

考點：菱形的性質，全等三角形的判定和性質，直角三角形的性質

點評：解答本題的關鍵是讀懂題意及圖形，正確作出輔助線，熟練運用直角三角形斜邊上的中線等于斜邊的一半解題.