


|


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案科目:初中數學 來源: 題型:


查看答案和解析>>
科目:初中數學 來源: 題型:
 某研究性學習小組在探究矩形的折紙問題時,將一塊直角三角板的直角頂點繞著矩形ABCD的對角線交點O旋轉(如圖所示).已知AB=8,BC=10,圖中M、N分別為直角三角板的直角邊與矩形ABCD的邊CD、BC的交點.問:是否存在某一旋轉位置,使得CM+CN等于
某研究性學習小組在探究矩形的折紙問題時,將一塊直角三角板的直角頂點繞著矩形ABCD的對角線交點O旋轉(如圖所示).已知AB=8,BC=10,圖中M、N分別為直角三角板的直角邊與矩形ABCD的邊CD、BC的交點.問:是否存在某一旋轉位置,使得CM+CN等于| 44 | 5 |
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源:2011-2012學年山東威海市八年級下期末模擬數學試卷(三)(帶解析) 題型:解答題
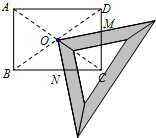
某研究性學習小組在探究矩形的折紙問題時,將一塊直角三角板的直角頂點繞矩形ABCD(AB<BC)的對角線的交點O旋轉(①→②→③),圖中的M、N分別為直角三角形的直角邊與矩形ABCD的邊CD、BC的交點。
⑴該學習小組成員意外的發現圖①(三角板一直角邊與OD重合)中,BN2=CD2+CN2,在圖③中(三角板一邊與OC重合),CN2=BN2+CD2,請你對這名成員在圖①和圖③中發現的結論選擇其一說明理由。
⑵試探究圖②中BN、CN、CM、DN這四條線段之間的數量關系,寫出你的結論,并說明理由。
⑶將矩形ABCD改為邊長為1的正方形ABCD,直角三角板的直角頂點繞O點旋轉到圖④,兩直角邊與AB、BC分別交于M、N,直接寫出BN、CN、CM、DM這四條線段之 間所滿足的數量關系(不需要證明)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com