
【題目】湖州素有魚米之鄉之稱,某水產養殖大戶為了更好地發揮技術優勢,一次性收購了![]()
![]() 淡水魚,計劃養殖一段時間后再出售.已知每天放養的費用相同,放養
淡水魚,計劃養殖一段時間后再出售.已知每天放養的費用相同,放養![]() 天的總成本為
天的總成本為![]() 萬元;放養
萬元;放養![]() 天的總成本為
天的總成本為![]() 萬元(總成本=放養總費用+收購成本).
萬元(總成本=放養總費用+收購成本).
(1)設每天的放養費用是![]() 萬元,收購成本為
萬元,收購成本為![]() 萬元,求
萬元,求![]() 和
和![]() 的值;
的值;
(2)設這批淡水魚放養![]() 天后的質量為
天后的質量為![]() (
(![]() ),銷售單價為
),銷售單價為![]() 元/
元/![]() .根據以往經驗可知:
.根據以往經驗可知:![]() 與
與![]() 的函數關系為
的函數關系為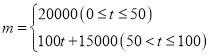 ;
;![]() 與
與![]() 的函數關系如圖所示.
的函數關系如圖所示.
①分別求出當![]() 和
和![]() 時,
時,![]() 與
與![]() 的函數關系式;
的函數關系式;
②設將這批淡水魚放養![]() 天后一次性出售所得利潤為
天后一次性出售所得利潤為![]() 元,求當
元,求當![]() 為何值時,
為何值時,![]() 最大?并求出最大值.(利潤=銷售總額-總成本)
最大?并求出最大值.(利潤=銷售總額-總成本)

【答案】(1)a的值為0.04,b的值為30(2)①y=![]() t+15,y=
t+15,y=![]() t+30②當t為55天時,W最大,最大值為180250元
t+30②當t為55天時,W最大,最大值為180250元
【解析】
試題分析:(1)根據題意,列方程組求解即可;
(2)①通過圖像找到相應的點的坐標,根據待定系數法分類列方程組求解即可得到函數的解析式;
然后根據利潤=銷售總額-總成本可列式=銷售單價×銷售天數-(放養總費用+收購成本),然后根據一次函數的特點和二次函數的最值求解即可.
試題解析:(1)由題意得![]()
解得![]()
答:a的值為0.04,b的值為30.
(2)①當0≤t≤50時,設y與t的函數關系式為y=k1t+n1
把點(0,15)和(50,25)的坐標分別代入y=k1t+n1,得
解得
∴y與t的函數關系式為y=![]() t+15
t+15
當50<t≤100時,設y與t的函數關系式為y=k2t+n2
把點(50,25)和(100,20)的坐標分別代入y=k2t+n2,得
解得
∴y與t的函數關系式為y=![]() t+30
t+30
②由題意得,當0≤t≤50時,
W=20000×(![]() t+15)-(400t+300000)=3600t
t+15)-(400t+300000)=3600t
∵3600>0,∴當t=50時,W最大值=180000(元)
當50<t≤100時,W=(100t+15000)(![]() t+30)-(400t+300000)=-10t2+1100t+150000=-10(t-55)2+180250
t+30)-(400t+300000)=-10t2+1100t+150000=-10(t-55)2+180250
∵-10<0,∴當t=55時,W最大值=180250
綜上所述,當t為55天時,W最大,最大值為180250元.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】榮慶公司計劃從商店購買同一品牌的臺燈和手電筒,已知購買一個臺燈比購買一個手電筒多用20元,若用400元購買臺燈和用160元購買手電筒,則購買臺燈的個數是購買手電筒個數的一半.
(1)求購買該品牌一個臺燈、一個手電筒各需要多少元?
(2)經商談,商店給予榮慶公司購買一個該品牌臺燈贈送一個該品牌手電筒的優惠,如果榮慶公司需要手電筒的個數是臺燈個數的2倍還多8個,且該公司購買臺燈和手電筒的總費用不超過670元,那么榮慶公司最多可購買多少個該品牌臺燈?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,已知一次函數y=﹣ ![]() x+6與x,y軸分別交于A,B兩點,點C(0,n)是y軸上一點,把坐標平面沿直線AC折疊,點B剛好落在x軸上,則點C的坐標是( )
x+6與x,y軸分別交于A,B兩點,點C(0,n)是y軸上一點,把坐標平面沿直線AC折疊,點B剛好落在x軸上,則點C的坐標是( )
A.(0,3)
B.(0, ![]() )
)
C.(0, ![]() )
)
D.(0, ![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為積極創建全國文明城市,某市對某路口的行人交通違章情況進行了![]() 天的調查,將所得數據繪制成如下統計圖(圖2不完整):
天的調查,將所得數據繪制成如下統計圖(圖2不完整):
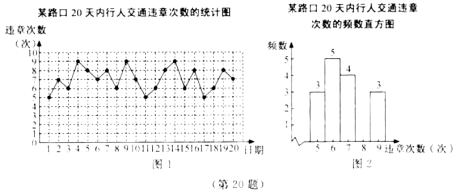
請根據所給信息,解答下列問題:
(1)第![]() 天,這一路口的行人交通違章次數是多少次?這
天,這一路口的行人交通違章次數是多少次?這![]() 天中,行人交通違章
天中,行人交通違章![]() 次的有多少天?
次的有多少天?
(2)請把圖2中的頻數直方圖補充完整;(溫馨提示:請畫在答題卷相對應的圖上)
(3)通過宣傳教育后,行人的交通違章次數明顯減少.經對這一路口的再次調查發現,平均每天的行人交通違章次數比第一次調查時減少了![]() 次,求通過宣傳教育后,這一路口平均每天還出現多少次行人的交通違章?
次,求通過宣傳教育后,這一路口平均每天還出現多少次行人的交通違章?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司今年如果用原線下銷售方式銷售一產品,每月的銷售額可達100萬元.由于該產品供不應求,公司計劃于3月份開始全部改為線上銷售,這樣,預計今年每月的銷售額y(萬元)與月份x(月)之間的函數關系的圖象如圖1中的點狀圖所示(5月及以后每月的銷售額都相同),而經銷成本p(萬元)與銷售額y(萬元)之間函數關系的圖象圖2中線段AB所示.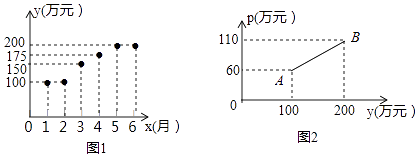
(1)求經銷成本p(萬元)與銷售額y(萬元)之間的函數關系式;
(2)分別求該公司3月,4月的利潤;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com