
【題目】如圖,在平面直角坐標系中,線段OA與線段OA′關于直線l:y=x對稱.已知點A的坐標為(2,1),則點A′的坐標為_____.
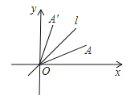
【答案】(1,2)
【解析】
如圖,過點A作AC⊥x軸于點C,過點A′作A′C′⊥y軸于點C′,連接AA′交直線l于點D,根據線段OA與線段OA′關于直線l:y=x對稱得出∠A′OD=∠AOD,OA′=OA,進而求出△A′C′O≌△ACO,即可得出點A′的坐標.
解:如圖,過點A作AC⊥x軸于點C,過點A′作A′C′⊥y軸于點C′,連接AA′交直線l于點D,
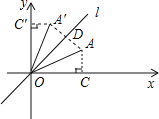
∵線段OA與線段OA′關于直線l:y=x對稱,
∴△ODA′≌△ODA,∠C′OD=∠DOC,
∴∠A′OD=∠AOD,OA′=OA,
∴在△A′C′O和△ACO中,
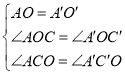 ,
,
∴△A′C′O≌△ACO,
∴AC=A′C′,CO=OC′,
∵點A的坐標為(2,1),
∴點A′的坐標為(1,2),
故答案為:(1,2).


科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知點![]() 的坐標為
的坐標為![]() ,且
,且![]() ,拋物線
,拋物線![]() 圖象經過
圖象經過![]() 三點.
三點.
(1)求![]() 兩點的坐標;
兩點的坐標;
(2)求拋物線的解析式;
(3)若點![]() 是直線
是直線![]() 下方的拋物線上的一個動點,作
下方的拋物線上的一個動點,作![]() 于點
于點![]() ,當
,當![]() 的值最大時,求此時點
的值最大時,求此時點![]() 的坐標及
的坐標及![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
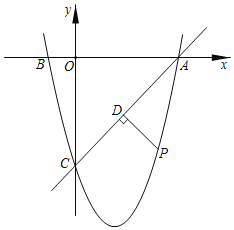
【題目】(本題10分)如圖,在平面直角坐標系xOy中,直線![]() 與y軸交于點C,與x軸交于點B,拋物線
與y軸交于點C,與x軸交于點B,拋物線![]() 經過B、C兩點,與x軸的正半軸交于另一點A,且OA :OC="2" :7.
經過B、C兩點,與x軸的正半軸交于另一點A,且OA :OC="2" :7.
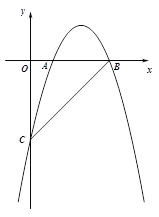


(1)求拋物線的解析式;
(2)點D為線段CB上,點P在對稱軸的右側拋物線上,PD=PB,當tan∠PDB=2,求P點的坐標;
(3)在(2)的條件下,點Q(7,m)在第四象限內,點R在對稱軸的右側拋物線上,若以點P、D、Q、R為頂點的四邊形為平行四邊形,求點Q、R的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
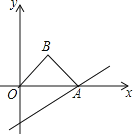
【題目】如圖,直線y=![]() x﹣2與x軸交于點A,以OA為斜邊在x軸的上方作等腰直角三角形OAB,將△OAB沿x軸向右平移,當點B落在直線y=
x﹣2與x軸交于點A,以OA為斜邊在x軸的上方作等腰直角三角形OAB,將△OAB沿x軸向右平移,當點B落在直線y=![]() x﹣2上時,則線段AB在平移過程中掃過部分的圖形面積為_____.
x﹣2上時,則線段AB在平移過程中掃過部分的圖形面積為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(探究證明)(1)某班數學課題學習小組對矩形內兩條互相垂直的線段與矩形兩鄰邊的數量關系進行探究,提出下列問題,請你給出證明:
如圖①,在矩形ABCD中,EF⊥GH,EF分別交AD、BC于點E、F,GH分別交AB、DC于點G、H,求證:![]() ;
;
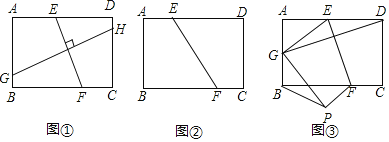
(結論應用)(2)如圖②,將矩形ABCD沿EF折疊,使得點B和點D重合,若AB=2,BC=3.求折痕EF的長;
(拓展運用)(3)如圖③,將矩形ABCD沿EF折疊.使得點D落在AB邊上的點G處,點C落在點P處,得到四邊形EFPG,若AB=2,BC=3,EF=![]() ,請求BP的長.
,請求BP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
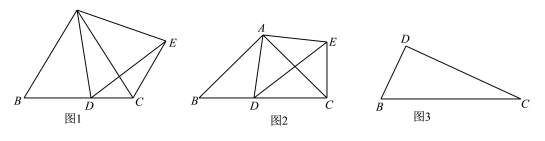
【題目】如圖1,在△ABC中,AB=AC,∠BAC=60°,D為BC邊上一點,(不與點B、C)重合,將線段AD繞點A逆時針旋轉60°得到AE,連接EC,則∠ACE的度數是__________,線段AC,CD,CE之間的數量關系是_______________.
(2)2,在△ABC中,AB=AC,∠BAC=90°,D為BC邊上一點(不與點B、C重合),將線段AD繞點A逆時針旋轉90°得到AE,連接EC,請寫出∠ACE的度數及線段AD,BD,CD之間的數量關系,并說明理由.
(3)如圖3,在Rt△DBC中,DB=3,DC=5,∠BDC=90°,若點A滿足AB=AC,∠BAC=90°,請直接寫出線段AD的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
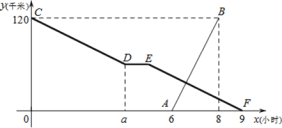
【題目】甲、乙兩地相距 120 千米,小張騎自行車從甲地出發勻速駛往乙地,出發 a小時開始休息,1 小時后仍按原速繼續行駛.小李比小張晚出發一段時間,騎摩托車從乙地勻速駛往甲地,圖中折線 CD-DE-EF,線段 AB 分別表示小張、小李與乙地的距離 y(千米)與小張出發時間 x(小時)之間的函數關系圖象.
(1)小李到達甲地后,再經過 小時小張到達乙地;小張騎自行車的速度是 千米/時;
(2)當 a=4 時,求小張與乙地的距離 y乙 與小張出發的時間 x(小時)之間的函數關系式;
(3)若小張恰好在休息期間與小李相遇,請直接寫出 a 的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
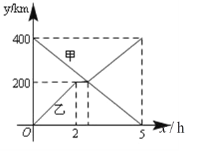
【題目】甲,乙兩輛汽車分別從A,B兩地同時出發,沿同一條公路相向而行,乙車出發2h后休息,與甲車相遇后,繼續行駛.設甲,乙兩車與B地的路程分別為y甲(km),y乙 (km),行駛的時間為x(h),y甲,y乙與x之間的函數圖象如圖所示,結合圖象解答下列問題:
(1)乙車休息了多長時間;
(2)求乙車與甲車相遇后y乙與x的函數解析式,并寫出自變量x的取值范圍;
(3)當兩車相距40km時,求出x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
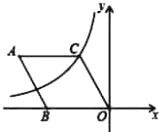
【題目】如圖,在菱形ABOC中,AB=2,∠A=60°,菱形的一個頂點C在反比例函數y=![]() (k≠0)的圖象上,則反比例函數的解析式為( )
(k≠0)的圖象上,則反比例函數的解析式為( )
A.y=![]() B.y=
B.y=![]() C.y=
C.y=![]() D.y=
D.y=![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com