
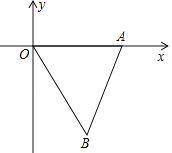
【題目】如圖,在平面直角坐標系中,點A與點B關于原點O對稱,點A![]() ,點C
,點C![]() ,點P在直線BC上運動.
,點P在直線BC上運動.
(1)連接AC、BC,求證:△ABC是等邊三角形;
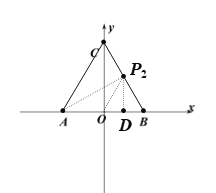
(2)求點P的坐標,使∠APO=![]() ;
;
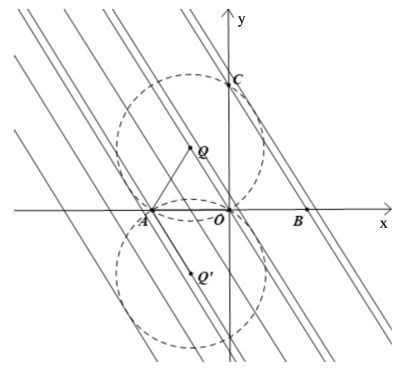
(3)在平面內,平移直線BC,試探索:當BC在不同位置時,使∠APO=![]() 的點P的個數是否保持不變?若不變,指出點P的個數有幾個?若改變,指出點P的個數情況,并簡要說明理由.
的點P的個數是否保持不變?若不變,指出點P的個數有幾個?若改變,指出點P的個數情況,并簡要說明理由.
【答案】(1)見解析;(2)(0,![]() ),(1,
),(1,![]() );(3)見解析.
);(3)見解析.
【解析】
(1)如圖(見解析),根據A、B、C三點的坐標求出AB、AC、BC的長,即可得證;
(2)由題(1)的結論可知,![]() ,因此當點P與點C重合,符合條件;如圖(見解析),取BC的中點
,因此當點P與點C重合,符合條件;如圖(見解析),取BC的中點![]() ,連接
,連接![]() ,由等邊三角形性質可得
,由等邊三角形性質可得![]() ,則
,則![]() ,故點
,故點![]() 也符合條件,最后根據
也符合條件,最后根據![]() 為BC邊上的中點即可求得其坐標;
為BC邊上的中點即可求得其坐標;
(3)因為以AO為弦畫圓,AO所對的圓心角等于![]() ,則根據圓周角定理得,直線BC與圓的交點P即為滿足條件的點,又因這樣的圓共有2個:如圖(見解析),逐一分析直線BC與兩圓的位置關系即可得.
,則根據圓周角定理得,直線BC與圓的交點P即為滿足條件的點,又因這樣的圓共有2個:如圖(見解析),逐一分析直線BC與兩圓的位置關系即可得.
(1)根據A、B、C三點的坐標可得:![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]()
則![]()
故![]() 是等邊三角形;
是等邊三角形;
(2)![]() 是等邊三角形
是等邊三角形
![]()
則當點P與點C重合,符合條件,此時P的坐標為![]() ;
;
當點P與點C不重合時,取BC的中點![]() ,連接
,連接![]()
由等邊三角形的性質得:![]()
![]() ,故點
,故點![]() 就是符合條件的點
就是符合條件的點
又![]()
![]() 是等邊三角形
是等邊三角形
過![]() 作
作![]()
![]()
![]() (
(![]() 是
是![]() 的中位線)
的中位線)
則點![]() 的坐標是
的坐標是![]()
綜上,所求點P的坐標為![]() ,
,![]() ;
;
(3)當BC在不同位置時,點P的個數會發生改變,使得![]() 的點P的個數情況共有4種:1個,2個,3個,4個,理由如下:
的點P的個數情況共有4種:1個,2個,3個,4個,理由如下:
如圖,以AO為弦畫圓,AO所對的圓心角等于![]() 的圓共有2個,記作圓Q和圓
的圓共有2個,記作圓Q和圓![]() ,顯然點Q和點
,顯然點Q和點![]() 關于x軸對稱
關于x軸對稱
因為直線BC與圓Q和圓![]() 的公共點P都滿足
的公共點P都滿足![]()
所以點P的個數情況如下:
①有1個:直線BC與圓Q(或圓![]() )相切
)相切
②有2個:直線BC與圓Q(或圓![]() )相交
)相交
③有3個:直線BC與圓Q(或圓![]() )相切,同時與圓
)相切,同時與圓![]() (或圓Q)相交;直線BC經過圓Q與圓
(或圓Q)相交;直線BC經過圓Q與圓![]() 的一個交點,同時與兩圓相交
的一個交點,同時與兩圓相交
④有4個:直線BC與圓Q,圓![]() 都相交,且不經過兩圓的交點.
都相交,且不經過兩圓的交點.


科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系xOy中,點A、B的坐標分別為(9,0)、(6,﹣9),△AB'O'是△ABO關于點A的位似圖形,且O'的坐標為(﹣3,0),則點B'的坐標為( )
A.(8,﹣12)B.(﹣8,12)
C.(8,﹣12)或(﹣8,12)D.(5,﹣12)
查看答案和解析>>
科目:初中數學 來源: 題型:
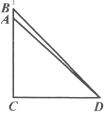
【題目】一輛從A站開往D站的動車,途中經停B、C兩站,互不相識的甲、乙、丙三人同時從A站上車。
(1)求甲、乙兩人在同一車站下車的概率;
(2)甲、乙、丙三人在同一車站下車的概率為
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】北京時間2019年3月10日0時28分,我國在西昌衛星發射中心用長征三號乙運載火箭,成功將中星![]() 衛星發射升空,衛星進入預定軌道.如圖,火星從地面
衛星發射升空,衛星進入預定軌道.如圖,火星從地面![]() 處發射,當火箭達到
處發射,當火箭達到![]() 點時,從位于地面雷達站
點時,從位于地面雷達站![]() 處測得
處測得![]() 的距離是
的距離是![]() ,仰角為
,仰角為![]() ;1秒后火箭到達
;1秒后火箭到達![]() 點,測得
點,測得![]() 的仰角為
的仰角為![]() .(參考數據:sin42.4°≈0.67,cos42.4°≈0.74,tan42.4°≈0.905,sin45.5°≈0.71,cos45.5°≈0.70,tan45.5°≈1.02)
.(參考數據:sin42.4°≈0.67,cos42.4°≈0.74,tan42.4°≈0.905,sin45.5°≈0.71,cos45.5°≈0.70,tan45.5°≈1.02)
(Ⅰ)求發射臺與雷達站之間的距離![]() ;
;
(Ⅱ)求這枚火箭從![]() 到
到![]() 的平均速度是多少(結果精確到0.01)?
的平均速度是多少(結果精確到0.01)?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,面積為1的等腰直角△OA1A2,∠OA2A1=90°,且OA2為斜邊在△OA1A2外作等腰直角△OA2A3,以OA3為斜邊在△OA2A3外作等腰直角△OA3A4,以OA4為斜邊在△OA3A4外作等腰直角△OA4A5,…連接A1A3,A3A5,A5A7,…分別與OA2,OA4,OA6,…交于點B1,B2,B3,…按此規律繼續下去,記△OB1A3的面積為S1,△OB2A5的面積為S2,△OB3A7的面積為S3,…△OBnA2n+1的面積為Sn,則Sn=__(用含正整數n的式子表示).

查看答案和解析>>
科目:初中數學 來源: 題型:
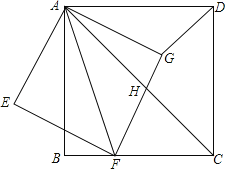
【題目】如圖,正方形ABCD中,點F是BC邊上一點,連結AF,以AF為對角線作正方形AEFG,邊FG與正方形ABCD的對角線AC相交于點H,連結DG.
(1)填空:若∠BAF=18°,則∠DAG=______°.
(2)證明:△AFC∽△AGD;
(3)若![]() =
=![]() ,請求出
,請求出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設直線y=kx+6和直線y=(k+1)x+6(k是正整數)及x軸圍成的三角形面積為Sk(k=1,2,3,…,8),則S1+S2+S3+…+S8的值是( )
A. ![]() B.
B. ![]() C. 16D. 14
C. 16D. 14
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com