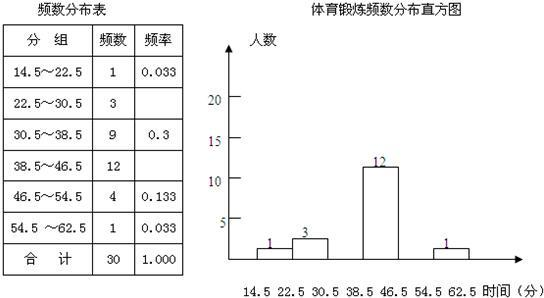
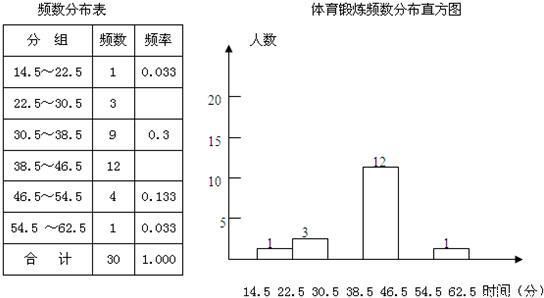
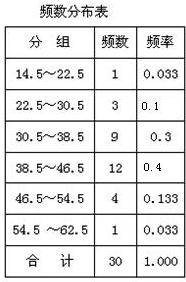
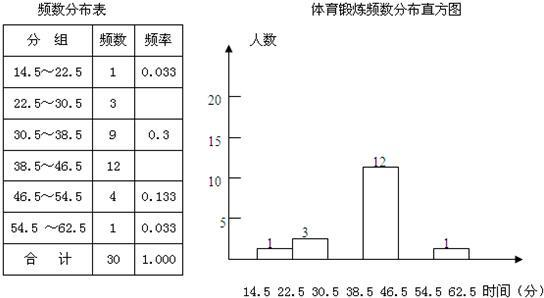
解:(1)樣本容量=9÷0.3=30,所以22.5-30.5的頻率=3÷30=0.1,38.5-46.5的頻率=12÷30=0.4,頻數分布表如圖:
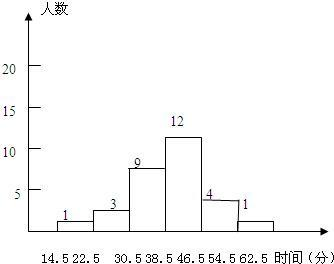
體育鍛煉頻數分布直方圖如圖:
(2)總體是實驗中學九年級300名學生平均每天參加課外鍛煉的時間,樣本是九年級30名學生平均每天參加課外鍛煉的時間;眾數是39,40;中位數是39;
(3)用平均數、眾數、中位數描述實驗中學300名學生平均每天參加課外鍛煉時間的總體情況都比較合適,因為在這一問題中這三個量非常接近;
(4)因為隨機調查的30名學生平均每天參加課外鍛煉的時間多于30分鐘的有26人,所以可以估計實驗中學平均每天參加課外鍛煉時間多于30分鐘的學生有
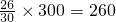
人.
分析:(1)先通過第3組計算出樣本容量,再用頻數除以總體得頻率,再畫圖;
(2)結合題意知,在這個問題中,總體是實驗中學九年級300名學生平均每天參加課外鍛煉的時間,樣本是九年級30名學生一周內平均每天參加課外鍛煉的時間;其中出現次數最多的數是眾數,即39,40;中位數先把所有的數據排序,再找中間的數;
(3)用平均數、眾數、中位數描述實驗中學300名學生平均每天參加課外鍛煉時間的總體情況都比較合適,因為在這一問題中這三個量非常接近;
(4)先找出平均每天參加課外鍛煉的時間多于30分鐘人數,求其頻率再乘以總人數即可.
點評:本題考查讀頻數分布表的能力和利用統計圖獲取信息的能力.同時考查中位數、眾數的求法:給定n個數據,按從小到大排序,如果n為奇數,位于中間的那個數就是中位數;如果n為偶數,位于中間兩個數的平均數就是中位數.任何一組數據,都一定存在中位數的,但中位數不一定是這組數據量的數.給定一組數據,出現次數最多的那個數,稱為這組數據的眾數.




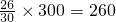 人.
人.