
 如圖,甲、乙兩人分別從A(1,$\sqrt{3}$),B(6,0)兩點同時出發,點O為坐標原點,甲沿AO方向,乙沿BO方向均以4km/h的速度行駛,th后,甲到達M點,乙到達N點.
如圖,甲、乙兩人分別從A(1,$\sqrt{3}$),B(6,0)兩點同時出發,點O為坐標原點,甲沿AO方向,乙沿BO方向均以4km/h的速度行駛,th后,甲到達M點,乙到達N點.分析 (1)判斷出甲、乙兩人到達O點前,只有當t=0時,△OMN∽△OAB,即可推得MN與AB不可能平行.
(2)根據題意,分三種情況:①t<$\frac{1}{2}$時;②當$\frac{1}{2}$<t<$\frac{3}{2}$時;③當t>$\frac{3}{2}$時;求出當t為何值時,△OMN∽△OBA.
(3)根據題意,分三種情況:①t≤$\frac{1}{2}$時;②當$\frac{1}{2}$<t≤$\frac{3}{2}$時;③當t>$\frac{3}{2}$時;寫出s與t之間的函數關系式即可.
解答 解:(1)∵A點的坐標為(1,$\sqrt{3}$),
∴OA=$\sqrt{{1}^{2}{+(\sqrt{3})}^{2}}$=2;
∵OM=2-4t,ON=6-4t,
∴當$\frac{2-4t}{2}$=$\frac{6-4t}{6}$時,解得t=0,
∴甲、乙兩人到達O點前,只有當t=0時,△OMN∽△OAB,
∴MN與AB不可能平行.
(2)∵甲到達O點的時間為t=$\frac{1}{2}$,乙到達O點的時間為t=$\frac{6}{4}$=$\frac{3}{2}$,
∴甲先到達O點,
∴t=$\frac{1}{2}$或t=$\frac{3}{2}$時,O、M、N三點不能連接成三角形.
①t<$\frac{1}{2}$時,
如果△OMN∽△OBA,則有$\frac{2-4t}{6}$=$\frac{6-4t}{2}$,
解得t=2>$\frac{1}{2}$,
∴△OMN不可能和△OBA相似.
②當$\frac{1}{2}$<t<$\frac{3}{2}$時,
∠MON>∠AOB,
顯然△OMN不可能和△OBA相似.
③當t>$\frac{3}{2}$時,
$\frac{4t-2}{6}$=$\frac{4t-6}{2}$,
解得t=2>$\frac{3}{2}$,
∴當t=2時,△OMN∽△OBA.
(3)①當t≤$\frac{1}{2}$時,如圖1,過點M作MH⊥x軸于點H,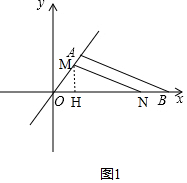 ,
,
在Rt△MOH中,
∵∠AOB=60°,
∴MH=OMsin60°=(2-4t)×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$(1-2t),
∴OH=OMcos60°=(2-4t)×$\frac{1}{2}$=1-2t,
∴NH=(6-4t)-(1-2t)=5-2t,
∴s=[$\sqrt{3}$(1-2t)]2+(5-2t)2
=3(4t2-4t+1)+(4t2-20t+25)
=16t2-32t+28.
②當$\frac{1}{2}$<t≤$\frac{3}{2}$時,如圖2,作MH⊥x軸于點H,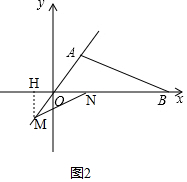 ,
,
在Rt△MOH中,
MH=$\frac{\sqrt{3}}{2}$(4t-2)=$\sqrt{3}$(2t-1),
NH=$\frac{1}{2}$(4t-2)+(6-4t)=5-2t,
∴s=[$\sqrt{3}$(1-2t)]2+(5-2t)2=16t2-32t+28.
③當t>$\frac{3}{2}$時,同理可得s=[$\sqrt{3}$(1-2t)]2+(5-2t)2=16t2-32t+28.
綜上,可得s=[$\sqrt{3}$(1-2t)]2+(5-2t)2=16t2-32t+28.
點評 此題主要考查了三角形相似的判定和性質的應用,要熟練掌握,解答此題的關鍵是要明確:①三邊法:三組對應邊的比相等的兩個三角形相似;②兩邊及其夾角法:兩組對應邊的比相等且夾角對應相等的兩個三角形相似;③兩角法:有兩組角對應相等的兩個三角形相似.


科目:初中數學 來源: 題型:解答題
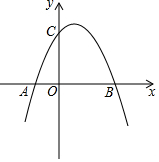 如圖,已知拋物線y=-x2+4x+5與x軸的兩個交點為A、B,與y軸交于點C.
如圖,已知拋物線y=-x2+4x+5與x軸的兩個交點為A、B,與y軸交于點C.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,扇形OAB的圓心角為90°,點C,D是弧AB的三等分點,半徑OC,OD分別與弦AB交于點E,F,下列說法錯誤的是( )
如圖,扇形OAB的圓心角為90°,點C,D是弧AB的三等分點,半徑OC,OD分別與弦AB交于點E,F,下列說法錯誤的是( )| A. | AE=EF=FB | B. | AC=CD=DB | C. | EC=FD | D. | ∠DFB=75° |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com