
【題目】如圖,在△ABC中,AB=BC,以AB為直徑的⊙O與AC交于點D,過D作DF⊥BC, 交AB的延長線于E,垂足為F.
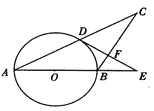
(1)求證:直線DE是⊙O的切線;
(2)當AB=5,AC=8時,求cosE的值.
【答案】(1)證OD⊥DE即可.(2)cosE=![]()
【解析】
試題如圖,在△ABC中,AB=BC,以AB為直徑的⊙O與AC交于點D,過D作DF⊥BC, 交AB的延長線于E,垂足為F.

(1)連結OD.易知OA=OD=r,且AB=BC,∴∠OAD=∠ODA=∠C
所以OD∥CB.所以∠ODE=∠BFE=90°.所以OD⊥DE,垂足為D.
所以直線DE是⊙O的切線.

(2)當AB=5,AC=8時,求cosE的值.
解:連結BD.由(1)知OD⊥DE,又因為∠ADB=90°(直徑所對圓周角)
所以∠ADO+∠ODB=∠ODB+∠BDE.因為OD∥CB,則∠ODB=∠DBO=∠DBF
所以Rt△ADB∽Rt△DFB.則![]() ,已知AB=BC,BD⊥AC.所以AD=
,已知AB=BC,BD⊥AC.所以AD=![]() AC=4.
AC=4.
所以在Rt△ADB中,BD=3.故3×3=5×BF,解得BF=![]() .易知Rt△EDO∽Rt△EFB
.易知Rt△EDO∽Rt△EFB
則![]() ,解得BE=
,解得BE=![]()
所以在Rt△EFB中,cosE=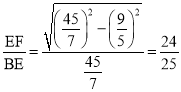


科目:初中數學 來源: 題型:
【題目】設二次函數y=(ax-1)(x-a),其中a是常數,且a≠0.
(1)當a=2時,試判斷點(-![]() ,-5)是否在該函數圖象上.
,-5)是否在該函數圖象上.
(2)若函數的圖象經過點(1,-4),求該函數的表達式.
(3)當![]() -1≤x≤
-1≤x≤![]() +1時,y隨x的增大而減小,求a的取值范圍.
+1時,y隨x的增大而減小,求a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】通過學習銳角三角比,我們知道在直角三角形中,一個銳角的大小與兩條邊長的比值是一一對應的,因此,兩條邊長的比值與角的大小之間可以相互轉化.類似的,可以在等腰三角形中建立邊角之間的聯系.我們定義:等腰三角形中底邊與腰的比叫做底角的鄰對(can),如圖(1)在△ABC中,AB=AC,底角B的鄰對記作canB,這時canB=底邊/腰=![]() ,容易知道一個角的大小與這個角的鄰對值也是一一對應的.根據上述角的鄰對的定義,解下列問題:
,容易知道一個角的大小與這個角的鄰對值也是一一對應的.根據上述角的鄰對的定義,解下列問題:
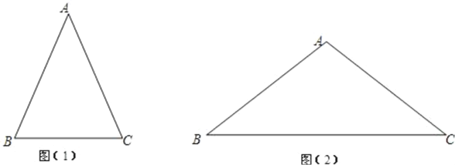
(1)can30°= ;
(2)如圖(2),已知在△ABC中,AB=AC,canB=![]() ,S△ABC=24,求△ABC的周長.
,S△ABC=24,求△ABC的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的紙箱里有分別標有漢字“熱”“愛”“祖”“國”的四個小球,除漢字不同之外,小球沒有任何區別,每次摸球前先搖勻再摸球.
(1)若從中任取一個球,求摸出球上的漢字剛好是“國”字的概率;
(2)小紅從中任取球,不放回,再從中任取一球,請用樹狀圖或列表法,求小紅取出的兩個球上的漢字恰好能組成“愛國”或“祖國”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在矩形ABCD中,點P是BC邊上一點,連接AP交對角線BD于點E,![]() .作線段AP的中垂線MN分別交線段DC,DB,AP,AB于點M,G,F,N.
.作線段AP的中垂線MN分別交線段DC,DB,AP,AB于點M,G,F,N.
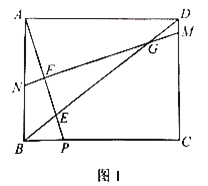
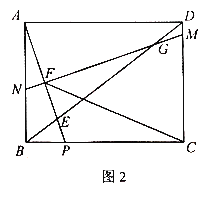
(1)求證:![]() ;
;
(2)若![]() ,求
,求![]() .
.
(3)如圖2,在(2)的條件下,連接CF,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從共享單車,共享汽車等共享出行到共享雨傘等共享物品,各式各樣的共享經濟模式在各個領域迅速的普及,根據國家信息中心發布的中國分享經濟發展報告2017顯示,參與共享經濟活動超6 億人,比上一年增加約1億人.
(1)為獲得北京市市民參與共享經濟活動信息,下列調查方式中比較合理的是 ;
A.對某學校的全體同學進行問卷調查
B.對某小區的住戶進行問卷調查
C.在全市里的不同區縣,選取部分市民進行問卷調查
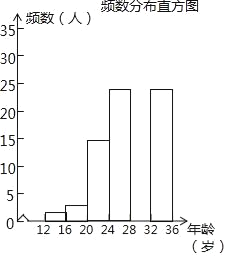
(2)調查小組隨機調查了延慶區市民騎共享單車情況,某社區年齡在12~36歲的人有1000人,從中隨機抽取了100人,統計了他們騎共享單車的人數,并繪制了如下不完整的統計圖表.如圖所示.騎共享單車的人數統計表
年齡段(歲) | 頻數 | 頻率 |
12≤x<16 | 2 | 0.02 |
16≤x<20 | 3 | 0.03 |
20≤x<24 | 15 | a |
24≤x<28 | 25 | 0.25 |
28≤x<32 | b | 0.30 |
32≤x<36 | 25 | 0.25 |
根據以上信息解答下列問題:
①統計表中的a= ;b= ;
②補全頻數分布直方圖;
③試估計這個社區年齡在20歲到32歲(含20歲,不含32歲)騎共享單車的人有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數![]() ,反比例函數
,反比例函數![]() (a,b,k是常數,且
(a,b,k是常數,且![]() ),若其中一部分x,y的對應值如表:則不等式
),若其中一部分x,y的對應值如表:則不等式![]() 的解集是_________.
的解集是_________.
x |
|
|
|
| 1 | 2 | 3 | 4 |
| 3 | 2 | 1 | 0 |
|
|
|
|
|
| 2 | 3 | 6 |
|
|
|
|
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了深入學習社會主義核心價值觀,對本校學生進行了一次相關知識的測試,隨機抽取了部分學生的測試成績進行統計(根據成績分為![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五個組,
五個組,![]() 表示測試成績,
表示測試成績,![]() 組:
組:![]() ;
;![]() 組:
組:![]() ;
;![]() 組:
組:![]() ;
;![]() 組:
組:![]() ;
;![]() 組:
組:![]() ),通過對測試成績的分析,得到如圖所示的兩幅不完整的統計圖,請你根據圖中提供的信息解答以下問題:
),通過對測試成績的分析,得到如圖所示的兩幅不完整的統計圖,請你根據圖中提供的信息解答以下問題:
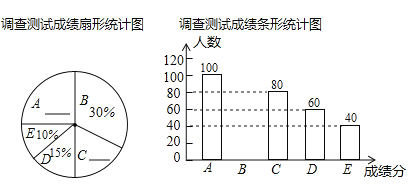
(1)抽取的學生共有______人,請將兩幅統計圖補充完整;
(2)抽取的測試成績的中位數落在______組內;
(3)本次測試成績在80分以上(含80分)為優秀,若該校初三學生共有1200人,請估計該校初三測試成績為優秀的學生有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
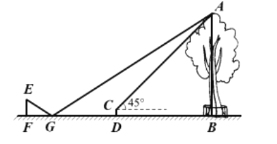
【題目】小明利用剛學過的測量知識來測量學校內一棵古樹的高度。一天下午,他和學習小組的同學帶著測量工具來到這棵古樹前,由于有圍欄保護,他們無法到達古樹的底部B,如圖所示。于是他們先在古樹周圍的空地上選擇一點D,并在點D處安裝了測量器DC,測得古樹的頂端A的仰角為45°;再在BD的延長線上確定一點G,使DG=5米,并在G處的地面上水平放置了一個小平面鏡,小明沿著BG方向移動,當移動帶點F時,他剛好在小平面鏡內看到這棵古樹的頂端A的像,此時,測得FG=2米,小明眼睛與地面的距離EF=1.6米,測傾器的高度CD=0.5米。已知點F、G、D、B在同一水平直線上,且EF、CD、AB均垂直于FB,求這棵古樹的高度AB。(小平面鏡的大小忽略不計)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com